Опыт Майкельсона — Морли показывает, что положение «скорость света в пустоте независимо от направления равна с должно иметь место во всех инерциальных системах. Что же мы имеем в действительности? Классический закон сложения скоростей,: если скорость света в одной инерциальной системе равна с, то в инерциальной системе, движущейся относительно первой со скоростью ѵ, его скорость будет с+v. Здесь налицо очевидное противоречие со специальным принципом относительности, вытекающим из опыта Майкельсона — Морли, который утверждает, что во всех инерциальных системах скорость света должна быть равна с. Новый принцип относительности противоречит старому закону сложения скоростей. Один из них должен оказаться неверным.Установлением нового принципа относительности было пройдено только полпути в создании специальной теории относительности. Если остановиться на этом, то все недоразумения по-прежнему останутся, они только изменят свою форму. Результат опыта Майкельсона — Морли теперь формально понятен: он находится в согласии с новым принципом относительности, но по существу все-таки ведет к противоречиям.
Опыт Майкельсона — Морли показывает, что положение «скорость света в пустоте независимо от направления равна с должно иметь место во всех инерциальных системах. Что же мы имеем в действительности? Классический закон сложения скоростей,: если скорость света в одной инерциальной системе равна с, то в инерциальной системе, движущейся относительно первой со скоростью ѵ, его скорость будет с+v. Здесь налицо очевидное противоречие со специальным принципом относительности, вытекающим из опыта Майкельсона — Морли, который утверждает, что во всех инерциальных системах скорость света должна быть равна с. Новый принцип относительности противоречит старому закону сложения скоростей. Один из них должен оказаться неверным.
Опыт Майкельсона — Морли показывает, что положение «скорость света в пустоте независимо от направления равна с должно иметь место во всех инерциальных системах. Что же мы имеем в действительности? Классический закон сложения скоростей,: если скорость света в одной инерциальной системе равна с, то в инерциальной системе, движущейся относительно первой со скоростью ѵ, его скорость будет с+v. Здесь налицо очевидное противоречие со специальным принципом относительности, вытекающим из опыта Майкельсона — Морли, который утверждает, что во всех инерциальных системах скорость света должна быть равна с. Новый принцип относительности противоречит старому закону сложения скоростей. Один из них должен оказаться неверным.
Выше мы видели, что справедливость классического закона сложения скоростей можно проверить опытным путем только для небольших скоростей. В том же, что этот закон пригоден и для случая, когда одно слагаемое будет очень большим, никто не может убедить физиков. Если возникло непреодолимое противоречие, то виновником его может оказаться и старый закон сложения скоростей, который, по-видимому, непригоден для сложения больших скоростей. Эйнштейн заменил классический закон сложения скоростей (1) новым, релятивистским законом сложения скоростей: складывая скорости u и v, получим скорость w, которая выражается формулой
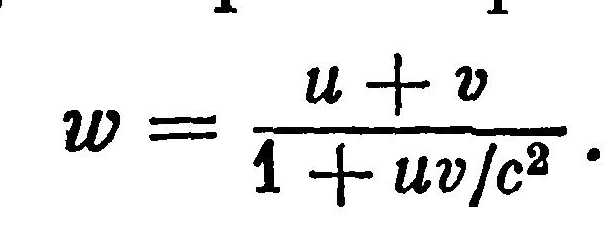 (2)
(2)Проанализируем эту формулу на конкретных примерах.
Пусть навстречу друг другу летят два реактивных самолета, каждый со скоростью (относительно Земли) 3 км/сек (т. е. и = 3 км/сек и ѵ = 3 км/сек). Какова скорость одного самолета относительно другого? Классическая формула (1) дает здесь простой ответ: скорость одного самолета относительно другого w = б км/сек. Если вычислять значение w по формуле (2), то получим w = 5,9999999994 км/сек, что ничтожно мало отличается от предыдущего результата. Имеющиеся в нашем распоряжении измерительные приборы не позволяют отличить скорость в 6 км/сек от скорости 5,9999999994 км/сек. Это означает, что при сложении двух скоростей, 3 км/сек каждая, обе формулы дают практически совпадающие результаты.
Нельзя забывать, что 3 км/сек в сравнении с масштабами обычной жизни очень большая величина. В повседневной жизни обычно мы встречаемся с много меньшими скоростями. Поэтому расхождение между результатами формул (1) и (2) при меньших скоростях будет еще
меньше. Так как вычисление по релятивистской формуле сложнее, чем по классической, а результаты с большой точностью совпадают, то в повседневной жизни целесообразнее использовать классический закон сложения скоростей. В принципе же релятивистская формула (2) дает более близкие к истине результаты, чем старая формула (1).
Посмотрим теперь, что говорит новая формула о сложении больших скоростей.
Пусть в космическом пространстве разминулись две частицы, скорости которых относительно Солнца 300 км/сек. Приверженец классической механики скажет, что скорость одной частицы относительно другой будет 600 км/сек. Сторонник теории относительности не согласится с этим. Используя формулу (2), он найдет скорость равной 599,9994 км/сек. Как видим, даже при таких больших скоростях, как 300 км/сек, релятивистская формула не дает существенно отличного по сравнению с классической формулой результата. При много больших скоростях разница становится уже заметной. Складывая две скорости по 100000 км/сек по релятивистской формуле, получим 180 000 км/сек. Это уже существенно отличается от результата классической формулы, которая дает 200000 км/сек. Чем больше скорости, которые мы будем складывать, тем больше становится эта разница. При сложении скоростей 200 000 и 200 000 км/сек получаем 277 000 км/сек, а не 400 000, как дает классическая формула; складывая же две скорости по 299 000 км/сек каждая, получаем только 299 788 (а не 598000) км/сек.
Особенно интересный результат получаем, пользуясь релятивистским законом сложения скоростей в том случае, когда одним из слагаемых является скорость света с. Заменим в формуле (2) u = с. Простое преобразование показывает, что w = с. Значит, если одной слагаемой скоростью будет скорость света, то в результате сложения опять получим скорость света. Если скорость света в одной инерциальной системе с, то в другой системе, движущейся относительно первой со скоростью v, его скорость также будет с, а не с + v, как утверждает классическая формула.
Релятивистская формула сложения скоростей так и выведена, чтобы закон: «скорость света в пустоте равна с» был пригоден во всех инерциальных системах. В то же время при сложении малых скоростей она с большой точностью дает тот же результат, что и классический закон сложения скоростей. Формула (2) находится в согласии как с нашим повседневным опытом, так и с измерениями, сделанными при определении скорости света. Классическая же формула, напротив, неточна и только приблизительно соответствует действительности. При сложении небольших скоростей она пригодна; в этом случае ошибка обычно не превышает точности измерений. При сложении же больших скоростей она дает совершенно неверные результаты.
Вопрос о сложении скоростей вовсе не такой простой, как мы считали раньше. На первый взгляд кажется непонятным, как скорости могут складываться соответственно с релятивистским законом. Таким же естественным, как «дважды два — четыре», кажется и требование, чтобы все скорости, малы они или велики, складывались по формуле (1). Такое убеждение укоренилось у людей потому, что мы живем в мире очень малых скоростей. Если бы мы привыкли к скоростям примерно 200000 км/сек, то вскоре убедились бы, что скорости в природе складываются именно так, как предписывает релятивистский закон сложения скоростей. Мы привыкли бы к этому закону, и вскоре он стал бы казаться нам таким же естественным и «очевидно правильным», каким сейчас кажется классический закон сложения скоростей.
Имея в виду, что в природе скорости складываются согласно релятивистской формуле (2), легко объяснить все результаты опытов, описанных в предыдущей главе.
Скорость компонента двойной звезды относительно Земли, складываясь со скоростью излученного им света, не изменяет последнюю. Скорость света будет с как относительно компонента звезды (источника света), так и относительно наблюдателя на Земле. Поэтому каких-либо кажущихся нерегулярностей в движении двойных звезд и не должно быть. Так же объясняется и результат опыта Майкельсона — Морли. Как бы мы ни измеряли скорость света, все равно результатом будет с (разумеется, в случае распространения света в пустоте), так как никакая скорость, складываясь со скоростью света, не меняет последнюю. Простые математические расчеты показывают, что результат опыта Физо также находится в согласии с релятивистским законом сложения скоростей.
Если скорость света в воде равна с/n, а скорость воды относительно земной поверхности равна v, то скорость света относительно земной поверхности по формуле (2) будет равна
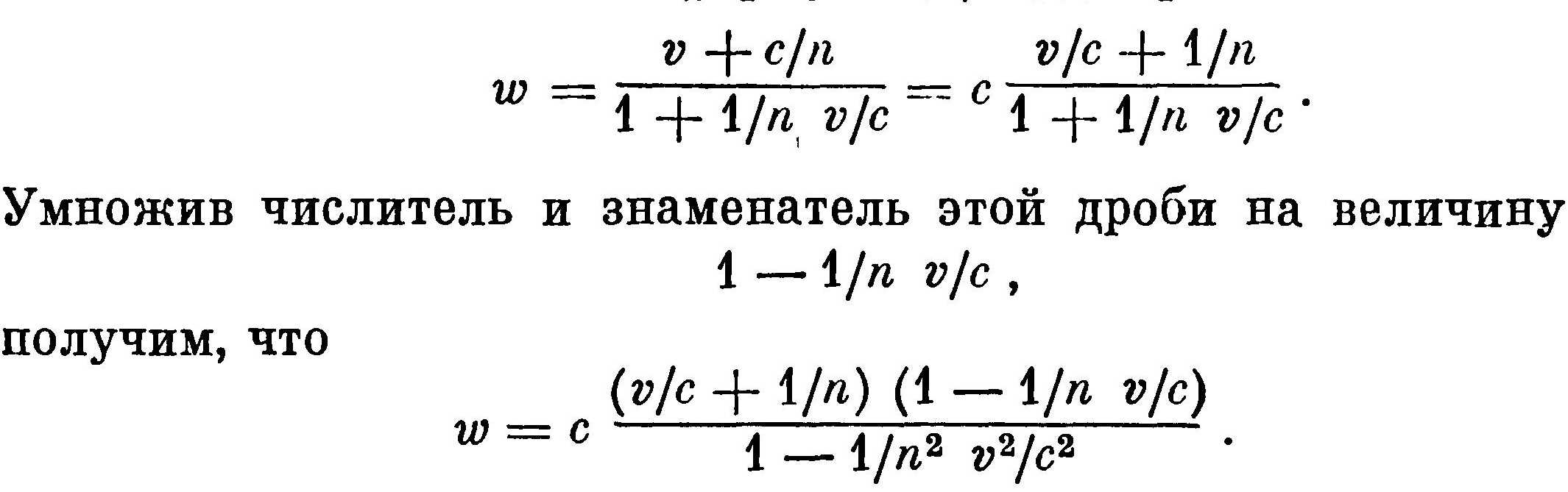
Скорость течения воды v очень мала по сравнению со скоростью света с, поэтому и величина ѵ/с очень мала, а ее квадрат (т. е. v2/с2) еще меньше. Физо в своем опыте не мог учесть такого
незначительного влияния, которое оказывает член, содержащий множитель v2/с2. Точность приборов для этого были недостаточной. Поэтому и мы в своих расчетах членами, содержащими v2/с2, будем пренебрегать. Пренебрегая в знаменателе предыдущей формулы вторым слагаемым, раскрыв скобки и отбросив члены, содержащие v2/с2, получим
w = с/n + ѵ (1 — 1/n2).
Такую же формулу получил и Физо из результатов своего опыта. Это показывает, что результат опыта Физо можно полностью объяснить с помощью релятивистского закона сложения скоростей.
Результат опыта Физо в свое время считали неоспоримым подтверждением наличия мирового эфира. После появления теории относительности оказалось, что опыт Физо подтверждает и ее. Но теория относительности категорически отрицала эфир вместе с абсолютной системой отсчета. Создалось интересное положение: один и тот же опыт как будто подтверждал две совершенно противоположные точки зрения. Основываясь только на опыте Физо, невозможно решить, которая из них верна.
По этому поводу М. Лауэ писал в своей книге «История физики» следующее: «История опыта Физо является поучительным примером того, какую большую роль в объяснении каждого опыта играют элементы теории; пх даже нельзя отделить от него. И если потом теории меняются, то опыт превращается из поразительного доказательства для одной теории в такой же сильный аргумент для противоположной теории?».