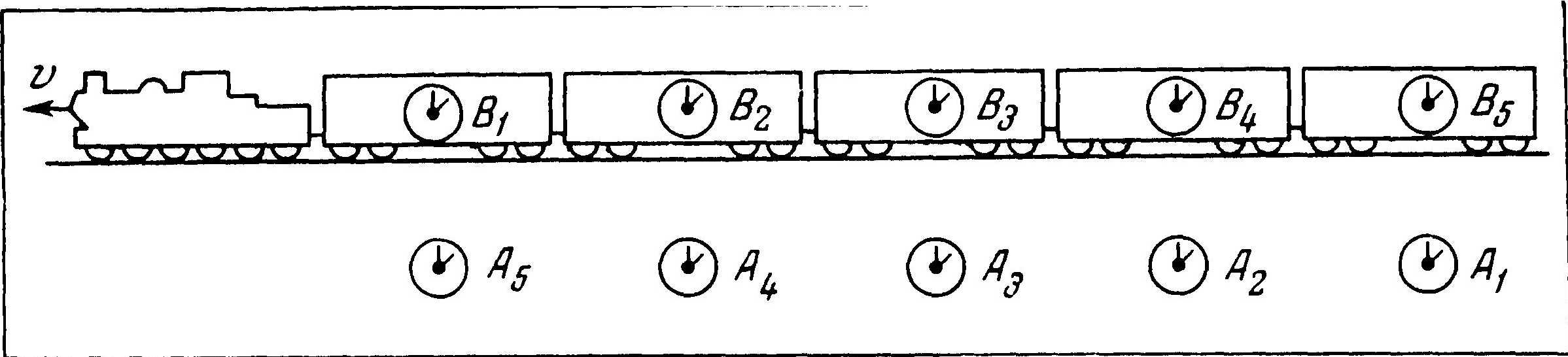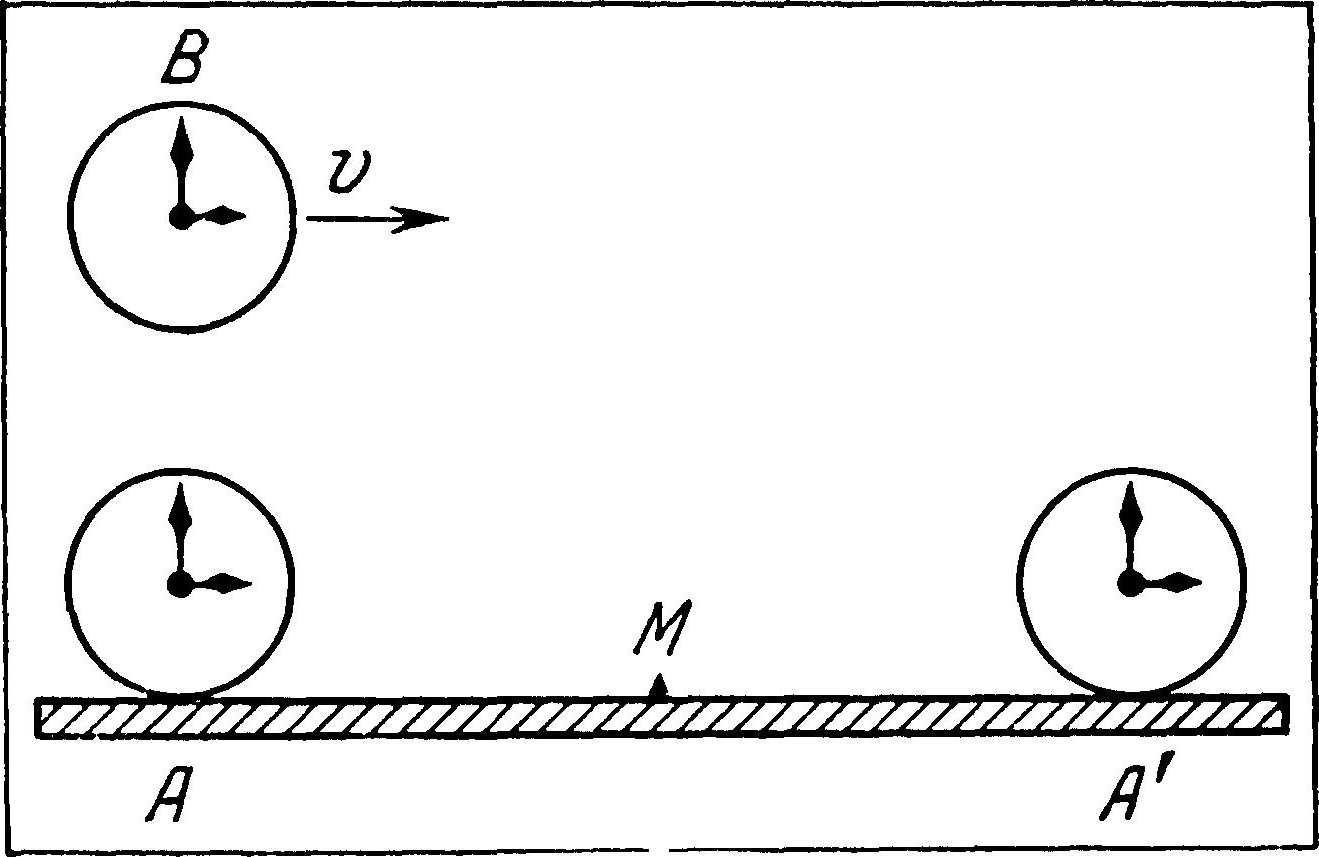

Читателю вся эта сложная система сравнения часов может показаться ненужной. У него может возникнуть такой вопрос: неужели действительно в разных инерциальных системах время может течь с различными скоростями? Может быть, на первый взгляд это и покажется крайне неправдоподобным, но все-таки дело обстоит именно так. Сравнение часов покажет, что для наблюдателя, находящегося у часов A, часы В идут медленнее, чем часы А. В движущейся инерциальной системе время течет медленнее, чем в покоящейся системе. Чтобы убедиться в сказанном, рассмотрим мысленно следующий опыт.
Пусть часы А и А\’ по-прежнему синхронизованы. Представим теперь, что в тот момент, когда часы В пройдут мимо часов л, от часов В испускается сигнал света. Пусть на своем пути сигнал встречает зеркало и, отразившись, возвращается к часам В как раз в тот момент, когда последние проходят мимо А\’ Луч света вернулся в то же самое место, откуда он и отправлялся, т. е. к часам В (рис. 26). В системе часов В луч света к зеркалу и обратно (от зеркала до часов В) пройдет по одной и той же прямой. Каким же будет путь луча света в системе отсчета часов A? Наблюдатель, находящийся у часов A, увидит, что луч света испускается от часов A, а возвращается обратно к часам А\’. В системе отсчета часов А луч света прошел вдоль равных сторон равнобедренного треугольника (рис. 27), и его путь в этой системе, следовательно, был длиннее пути светового луча в системе отсчета часов В. Выше мы видели, что скорость света во всех инерциальных системах одинакова и равна с, значит она будет равна с в системах отсчета, связанных и с часами А и с часами В. Отсюда следует, что относительно часов В луч света находился в пути меньшее время, чем относительно часов А, т. е. часы В успели отсчитать меньшее время. Значит, движущиеся часы В идут медленнее, чем покоящиеся часы А.
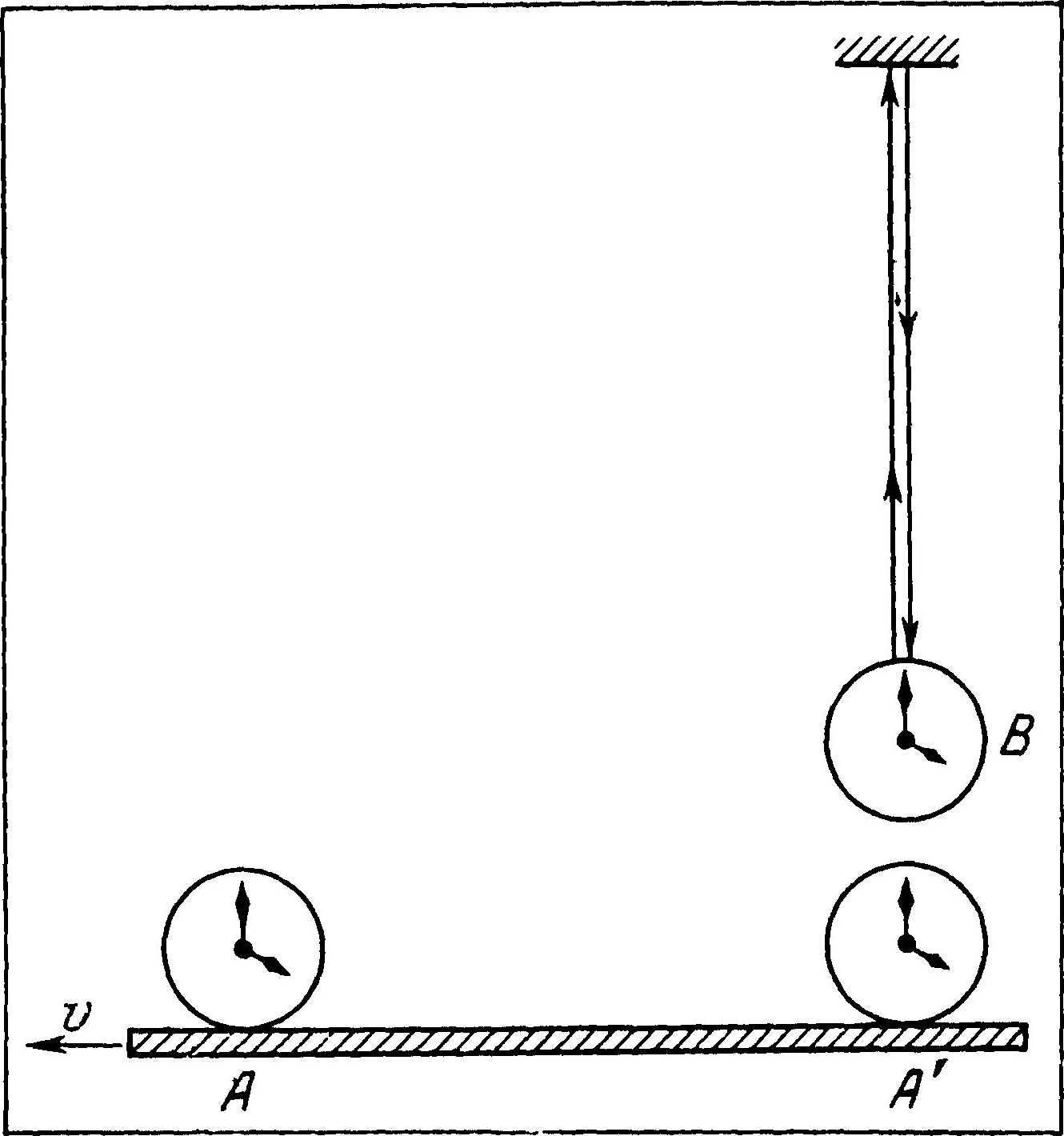
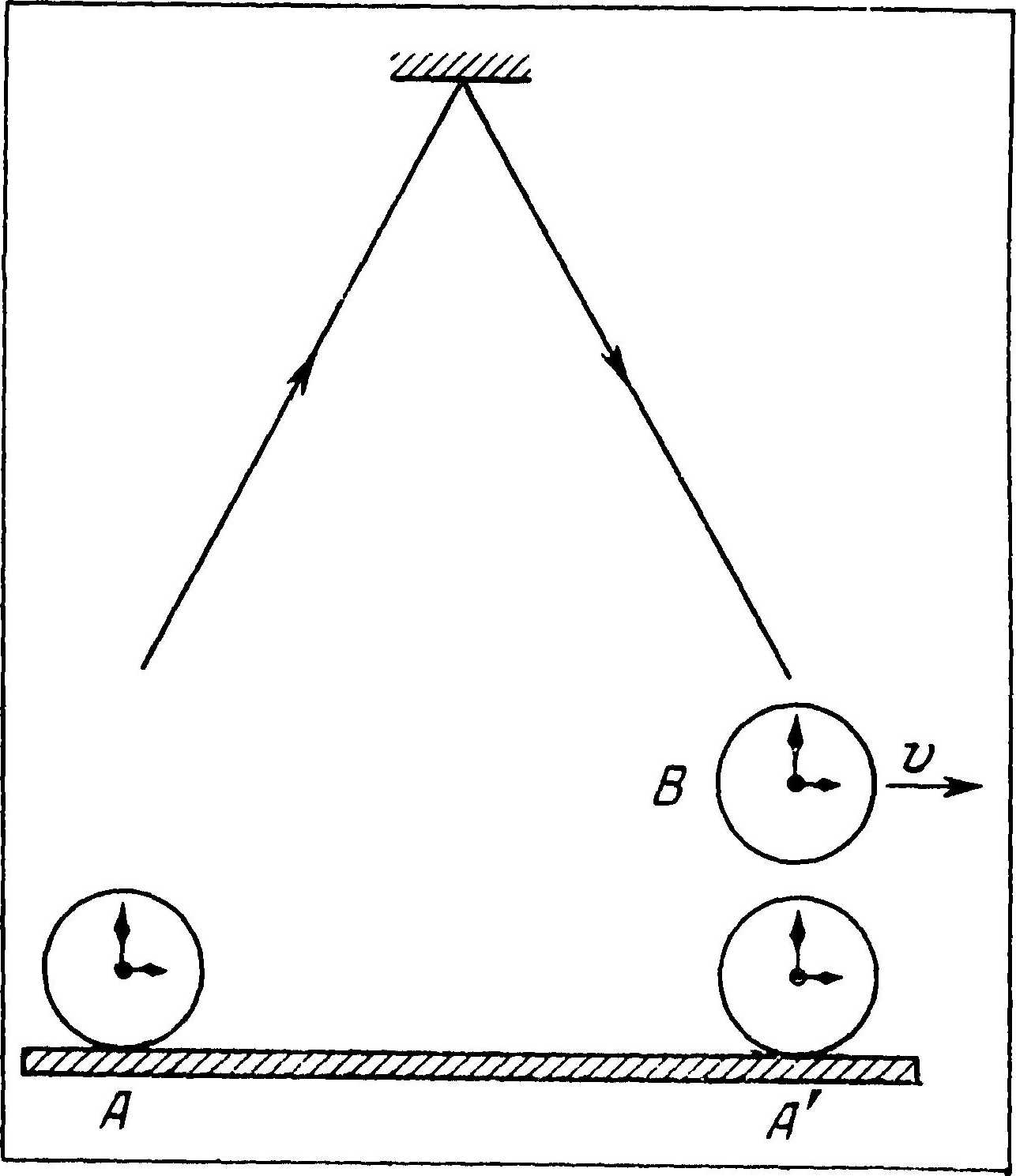
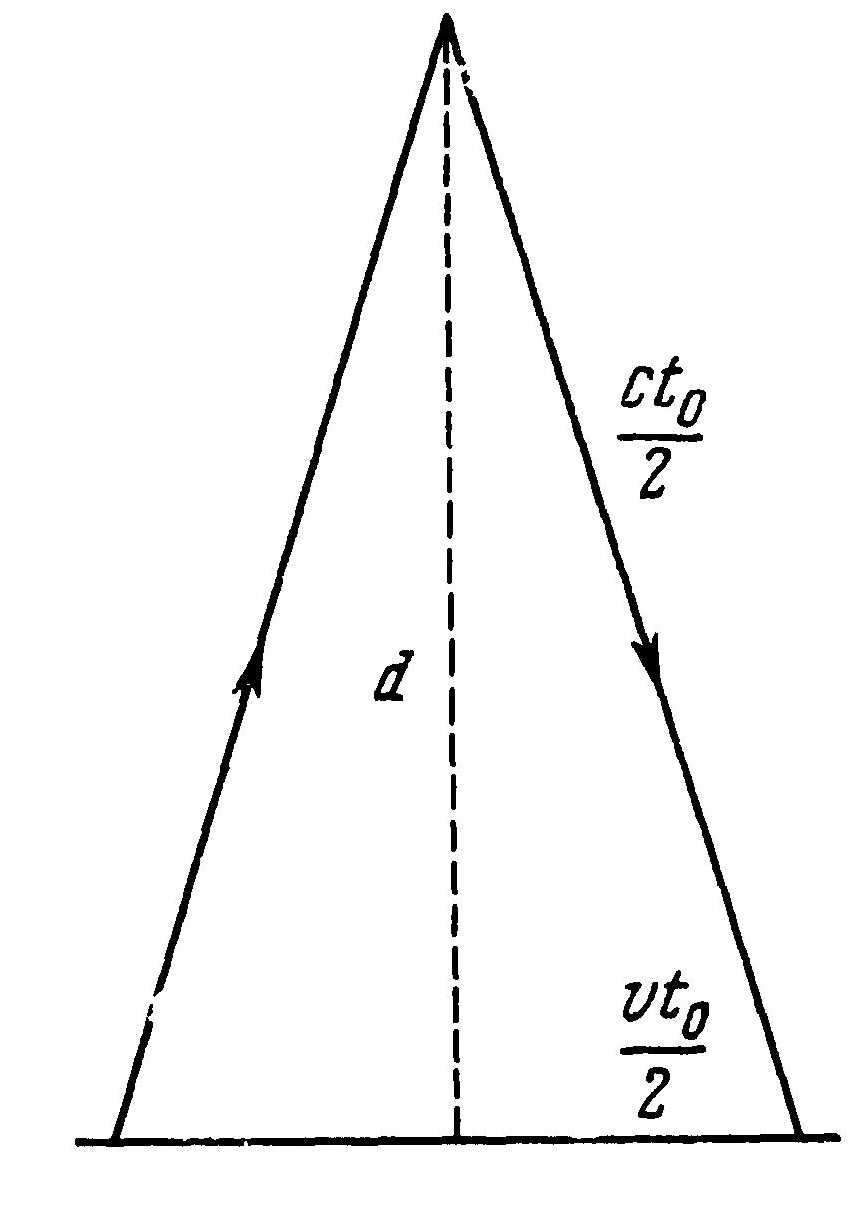
Рис. 28. Путь светового луча от часов В до зеркала и обратно для наблюдателя у часов А (сплошная линия) и для наблюдателя у часов В (пунктирная линия)
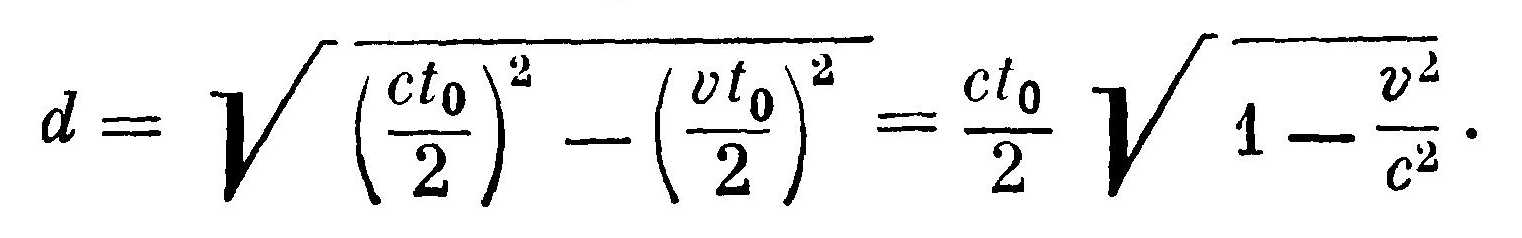
d = ct/2
Сравнивая эти два выражения для d, найдем, что
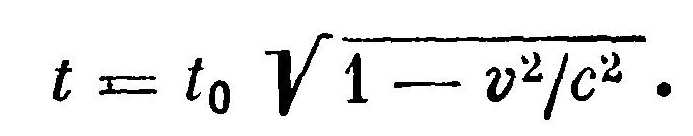 (3)
(3) Мы получим формулу, которая показывает, как промежуток времени, измеренный движущимися со скоростью v часами В, связан с промежутком времени t0, измеренным покоящимися часами А и А\’. Каждые часы измеряют время в связанной с ними системе отсчета. Следовательно, в системе часов В время течет медленнее (промежуток между событиями короче), чем в системе, связанной с часами А.
У читателя теперь может возникнуть впечатление, что, развивая теорию относительности, мы зашли в тупик. В самом деле, как же все инерциальные системы могут быть равноправными, если в одной из них время течет быстрее, а в другой медленнее? Получается, будто мы можем найти систему отсчета, в которой время течет быстрее, чем во всех остальных. Эта система была бы, очевидно, в исключительном положении по сравнению с другими системами, что противоречит принципу относительности. В действительности же никакого противоречия не возникает.
В приведенном выше примере наблюдатель был неподвижным относительно часов А и А\’ (иначе он не смог бы синхронизировать эти часы). Сравнивая ход часов А и В, т, е. скорости течения времени в связанных с ними системах отсчета, он пришел к выводу, что движущиеся часы В идут медленнее покоящихся часов А. Рассмотрим теперь, к какому выводу о ходе часов придет наблюдатель, неподвижный относительно часов В. Чтобы сравнить ход часов А и В, у него тоже должны быть вспомогательные часы. Может ли он в качестве вспомогательных часов использовать часы А\’? Простое рассуждение показывает, что не может.
Часы A и A\’ были синхронизированы наблюдателем, неподвижным по отношению к ним. Это значит, что для наблюдателя, находившегося посередине между часами А и A\’, стрелки этих часов были одновременно в одинаковых положениях. Но в предыдущем параграфе мы выяснили, что одновременность событий — понятие относительное: события, одновременные, например, для наблюдателя в системе часов А, не будут одновременными
в системе часов В. Для наблюдателя в системе отсчета часов В стрелки часов А и А\’ будут находиться в одинаковых положениях в разные моменты времени и ими пользоваться для сравнения нельзя. Если наблюдатель, неподвижный относительно часов В, хочет сравнить ход часов А и В, он должен взять вспомогательные часы В\’ неподвижные и синхронные по отношению к часам В. Рассуждая дальше так же, как это мы уже делали выше, мы сможем убедиться в том, что часы А идут медленнее часов В.
Следовательно, для наблюдателя, неподвижного относительно часов A, часы A идут быстрее часов В; для наблюдателя же, неподвижного относительно часов 5, часы В
идут быстрее часов A. Тем самым инерциальные системы отсчета, связанные с часами A и В, находятся в совершенно одинаковых условиях. В обоих случаях имеет место один и тот же закон природы: часы, неподвижные относительно системы, идут быстрее всех; движущиеся же часы идут тем медленнее, чем больше их скорость в данной системе. Значит мы не нарушили принципа относительности, который требует равноправности всех систем отсчета.