Со времен Кеплера известно, что планеты движутся вокруг Солнца по эллиптическим орбитам. Когда расстояние планеты от Солнца становится наименьшем, говорят, что планета находится в перигелии своей орбиты. Ньютон был твердо уверен, что точка перигелия покоится в пространстве, т. е. планеты все время обращаются по неподвижным эллипсам. Однако более поздние наблюдения обнаружили нечто иное. Оказалось, что с каждым оборотом планеты ее перигелий несколько смещается в направлении движения; таким образом, орбита планеты не является замкнутым эллипсом, а напоминает розетку (рис. 54).
Впервые движение перигелия было открыто у Меркурия. Сравнение данных старых наблюдений с новыми показало, что точка перигелия орбиты Меркурия сместилась за сто лет приблизительно на 565,3 секунды дуги в направлении движения планеты. Леверье занялся отысканием причины этого смещения. Выяснилось, что основная часть смещения была обусловлена влиянием других планет, главным образом Венеры и Земли. Воздействие всех планет, однако, вызвало сдвиг перигелия только на 527 секунд дуги за столетие. Расхождение на 38,3 секунды дуги, так называемое остаточное увеличение периге лия, было загадкой, которая долгие годы приковывала внимание ученых.
Впервые движение перигелия было открыто у Меркурия. Сравнение данных старых наблюдений с новыми показало, что точка перигелия орбиты Меркурия сместилась за сто лет приблизительно на 565,3 секунды дуги в направлении движения планеты. Леверье занялся отысканием причины этого смещения. Выяснилось, что основная часть смещения была обусловлена влиянием других планет, главным образом Венеры и Земли. Воздействие всех планет, однако, вызвало сдвиг перигелия только на 527 секунд дуги за столетие. Расхождение на 38,3 секунды дуги, так называемое остаточное увеличение периге лия, было загадкой, которая долгие годы приковывала внимание ученых.
Со времен Кеплера известно, что планеты движутся вокруг Солнца по эллиптическим орбитам. Когда расстояние планеты от Солнца становится наименьшем, говорят, что планета находится в перигелии своей орбиты. Ньютон был твердо уверен, что точка перигелия покоится в пространстве, т. е. планеты все время обращаются по неподвижным эллипсам. Однако более поздние наблюдения обнаружили нечто иное. Оказалось, что с каждым оборотом планеты ее перигелий несколько смещается в направлении движения; таким образом, орбита планеты не является замкнутым эллипсом, а напоминает розетку (рис. 54).
Впервые движение перигелия было открыто у Меркурия. Сравнение данных старых наблюдений с новыми показало, что точка перигелия орбиты Меркурия сместилась за сто лет приблизительно на 565,3 секунды дуги в направлении движения планеты. Леверье занялся отысканием причины этого смещения. Выяснилось, что основная часть смещения была обусловлена влиянием других планет, главным образом Венеры и Земли. Воздействие всех планет, однако, вызвало сдвиг перигелия только на 527 секунд дуги за столетие. Расхождение на 38,3 секунды дуги, так называемое остаточное увеличение периге лия, было загадкой, которая долгие годы приковывала внимание ученых.
Впервые движение перигелия было открыто у Меркурия. Сравнение данных старых наблюдений с новыми показало, что точка перигелия орбиты Меркурия сместилась за сто лет приблизительно на 565,3 секунды дуги в направлении движения планеты. Леверье занялся отысканием причины этого смещения. Выяснилось, что основная часть смещения была обусловлена влиянием других планет, главным образом Венеры и Земли. Воздействие всех планет, однако, вызвало сдвиг перигелия только на 527 секунд дуги за столетие. Расхождение на 38,3 секунды дуги, так называемое остаточное увеличение периге лия, было загадкой, которая долгие годы приковывала внимание ученых.
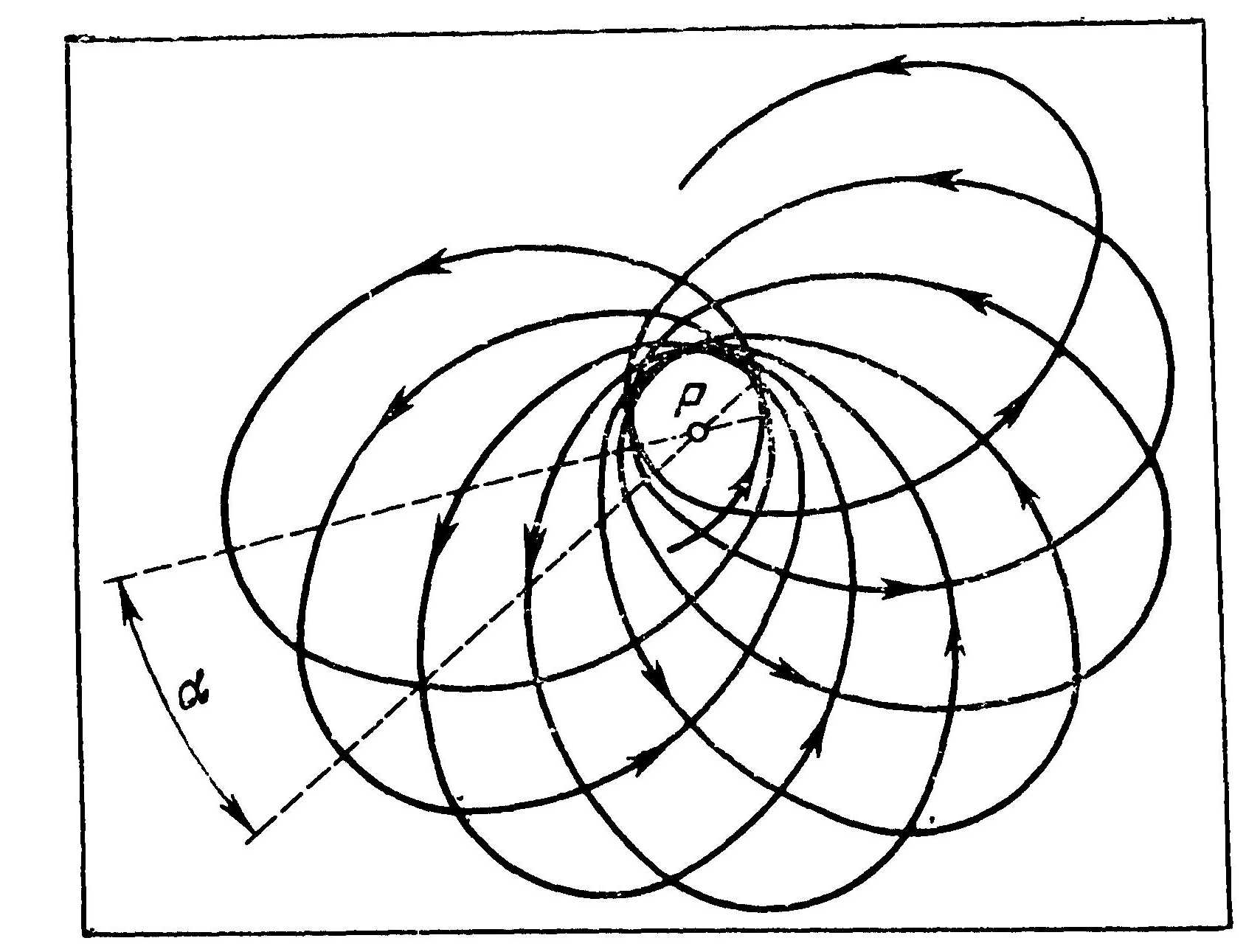
Рис. 54. Орбита вращения планеты вокруг Солнца Р. Угол а обозначает смещение перигелия за один оборот
В уточнении движения перигелия Меркурия большая заслуга принадлежит американскому астроному Ньюко-му. Его вычисления в конце прошлого столетия показали, что остаточное движение перигелия Меркурия равно 42,2 ± 2,1 секунды дуги за столетие. Более поздние исследования внесли в это значение совсем небольшую поправку и сейчас остаточное движение перигелия Меркурия считают равным 42,56 ± 0,94 секунды за столетие. Вычисления Ньюкома показывали существование остаточного движения перигелия не только у Меркурия, но и у Венеры и Марса. Для Венеры оно равно 10,1 ± 2,9, для Марса — 8,0 ± 3,7 секунд дуги за столетие. Но так как эти числа были относительно малы, то основное внимание исследователи по-прежнему уделяли Меркурию.
Чего только ни делалось для объяснения странного поведения Меркурия! Так, например, Леверье предполагал, что внутри орбиты Меркурия должна двигаться еще одна планета, которая и вызывает остаточное движение перигелия. Эта гипотеза не подтвердилась. Выяснилось, что такая планета должна была бы получаться на многочисленных фотографиях окрестностей Солнца. Тогда гипотезу Леверье несколько видоизменили, предположив, что в непосредственной близости от Солнца движется огромное количество малых планет, не оставляющих на фотопластинке следов. И это объяснение оказалось неправильным. Выяснилось, что такой пояс маленьких планет должен оказывать сильное возмущающее влияние и на Венеру, чего, однако, не обнаружили. Был сделан еще целый ряд попыток объяснить остаточное движение перигелия Меркурия. Так, например, предполагали, что возмущение обусловлено сплющенностью Солнца или наличием у Меркурия спутника. Но и эти попытки не выдержали серьезной критики.
Самой успешной поначалу казалась теория Зеелигера (1906 г.), в которой остаточное движение перигелия Меркурия объяснялось наличием движущейся между планетами солнечной системы космической пыли. Путем подходящего выбора плотности космической пыли автору удалось объяснить остаточное движение перигелия как Меркурия, так Венеры и Марса. Но и эта теория имела свою ахиллесову пяту. Фотометрические наблюдения показали, что плотность космической пыли в сто миллионов раз меньше, чем предполагал Зеелигер.
Самыми интересными по содержанию были относящиеся к концу прошлого столетия попытки Ньюкома, который хотел уточнить закон тяготения Ньютона. Уже самого Ньютона интересовало, не должно ли в формуле закона тяготения вместо показателя степени «2» стоять какое-то другое число n, незначительно отличающееся от 2. Тогда закон выражался бы в виде
F=γ * mM/rn
Вычисления Ньютона показали, что в том случае, если п не равно точно 2, то в движении планет должно наблюдаться смещение перигелия. В те времена смещение перигелия еще не было обнаружено, и отсюда Ньютон сделал вывод, что показатель степени в формуле закона тяготения должен быть в точности равен 2. Ныоком показал, что остаточное движение Меркурия можно объяснить, если предположить, что n = 2,00000016. Попытка Ньюкома не увенчалась успехом. Оказалось, что для объяснения движения Луны необходимо предположить, что п меньше 2,00000004. Отсюда следовало, что исправленная формула не может правильно описывать ни движение Меркурия, ни Луны. Загадка Меркурия оставалась неразрешенной.
Чего только ни делалось для объяснения странного поведения Меркурия! Так, например, Леверье предполагал, что внутри орбиты Меркурия должна двигаться еще одна планета, которая и вызывает остаточное движение перигелия. Эта гипотеза не подтвердилась. Выяснилось, что такая планета должна была бы получаться на многочисленных фотографиях окрестностей Солнца. Тогда гипотезу Леверье несколько видоизменили, предположив, что в непосредственной близости от Солнца движется огромное количество малых планет, не оставляющих на фотопластинке следов. И это объяснение оказалось неправильным. Выяснилось, что такой пояс маленьких планет должен оказывать сильное возмущающее влияние и на Венеру, чего, однако, не обнаружили. Был сделан еще целый ряд попыток объяснить остаточное движение перигелия Меркурия. Так, например, предполагали, что возмущение обусловлено сплющенностью Солнца или наличием у Меркурия спутника. Но и эти попытки не выдержали серьезной критики.
Самой успешной поначалу казалась теория Зеелигера (1906 г.), в которой остаточное движение перигелия Меркурия объяснялось наличием движущейся между планетами солнечной системы космической пыли. Путем подходящего выбора плотности космической пыли автору удалось объяснить остаточное движение перигелия как Меркурия, так Венеры и Марса. Но и эта теория имела свою ахиллесову пяту. Фотометрические наблюдения показали, что плотность космической пыли в сто миллионов раз меньше, чем предполагал Зеелигер.
Самыми интересными по содержанию были относящиеся к концу прошлого столетия попытки Ньюкома, который хотел уточнить закон тяготения Ньютона. Уже самого Ньютона интересовало, не должно ли в формуле закона тяготения вместо показателя степени «2» стоять какое-то другое число n, незначительно отличающееся от 2. Тогда закон выражался бы в виде
F=γ * mM/rn
Вычисления Ньютона показали, что в том случае, если п не равно точно 2, то в движении планет должно наблюдаться смещение перигелия. В те времена смещение перигелия еще не было обнаружено, и отсюда Ньютон сделал вывод, что показатель степени в формуле закона тяготения должен быть в точности равен 2. Ныоком показал, что остаточное движение Меркурия можно объяснить, если предположить, что n = 2,00000016. Попытка Ньюкома не увенчалась успехом. Оказалось, что для объяснения движения Луны необходимо предположить, что п меньше 2,00000004. Отсюда следовало, что исправленная формула не может правильно описывать ни движение Меркурия, ни Луны. Загадка Меркурия оставалась неразрешенной.