Относительна не только скорость, но и траектория тела. Чтобы в этом убедиться, понаблюдаем за пассажиром
в поезде, движущемся по прямому пути с постоянной скоростью. Пусть пассажир бросит из окна вагона тяжелый камень. По какому пути падает камень на землю?
По инерции камень продолжает движение с такой же скоростью, как и вагон, т. е. камень все время остается напротив окна вагона. В то же самое время он падает вниз. Человек, сидящий в поезде, скажет, что камень падает на землю по вертикальной прямой. Может ли то же самое сказать человек, стоящий у полотна железной дороги? Нет, не может. Он видит, что камень продолжает движение в направлении движения поезда, падая в то же время вниз. Выброшенный из окна вагона камень летит, как и брошенное горизонтально тело, по параболе. Траектория камня будет параболой, так будет утверждать человек, стоящий у полотна.
Не имеет смысла спрашивать, какова «действительная» траектория камня — прямая или парабола. Траектория тела не абсолютное понятие, о траектории можно говорить только относительно заданного тела отсчета. В разных системах отсчета траектория будет иметь различный вид. В то время как в системе отсчета, связанной с движущимся поездом, траекторией камня является прямая, в системе отсчета, связанной с Землей, она оказывается параболой. Траектория, как и скорость,— понятие относительное. О форме траектории имеет смысл говорить только после того, как будет фиксирована система отсчета.
в поезде, движущемся по прямому пути с постоянной скоростью. Пусть пассажир бросит из окна вагона тяжелый камень. По какому пути падает камень на землю?
По инерции камень продолжает движение с такой же скоростью, как и вагон, т. е. камень все время остается напротив окна вагона. В то же самое время он падает вниз. Человек, сидящий в поезде, скажет, что камень падает на землю по вертикальной прямой. Может ли то же самое сказать человек, стоящий у полотна железной дороги? Нет, не может. Он видит, что камень продолжает движение в направлении движения поезда, падая в то же время вниз. Выброшенный из окна вагона камень летит, как и брошенное горизонтально тело, по параболе. Траектория камня будет параболой, так будет утверждать человек, стоящий у полотна.
Не имеет смысла спрашивать, какова «действительная» траектория камня — прямая или парабола. Траектория тела не абсолютное понятие, о траектории можно говорить только относительно заданного тела отсчета. В разных системах отсчета траектория будет иметь различный вид. В то время как в системе отсчета, связанной с движущимся поездом, траекторией камня является прямая, в системе отсчета, связанной с Землей, она оказывается параболой. Траектория, как и скорость,— понятие относительное. О форме траектории имеет смысл говорить только после того, как будет фиксирована система отсчета.
Относительна не только скорость, но и траектория тела. Чтобы в этом убедиться, понаблюдаем за пассажиром
в поезде, движущемся по прямому пути с постоянной скоростью. Пусть пассажир бросит из окна вагона тяжелый камень. По какому пути падает камень на землю?
По инерции камень продолжает движение с такой же скоростью, как и вагон, т. е. камень все время остается напротив окна вагона. В то же самое время он падает вниз. Человек, сидящий в поезде, скажет, что камень падает на землю по вертикальной прямой. Может ли то же самое сказать человек, стоящий у полотна железной дороги? Нет, не может. Он видит, что камень продолжает движение в направлении движения поезда, падая в то же время вниз. Выброшенный из окна вагона камень летит, как и брошенное горизонтально тело, по параболе. Траектория камня будет параболой, так будет утверждать человек, стоящий у полотна.
Не имеет смысла спрашивать, какова «действительная» траектория камня — прямая или парабола. Траектория тела не абсолютное понятие, о траектории можно говорить только относительно заданного тела отсчета. В разных системах отсчета траектория будет иметь различный вид. В то время как в системе отсчета, связанной с движущимся поездом, траекторией камня является прямая, в системе отсчета, связанной с Землей, она оказывается параболой. Траектория, как и скорость,— понятие относительное. О форме траектории имеет смысл говорить только после того, как будет фиксирована система отсчета.
Можно привести множество примеров, демонстрирующих, что понятие траектории относительно. Так, например, орбита планеты Марс по отношению к Солнцу — эллипс, относительно же Земли орбита будет иметь гораздо более сложный вид (она состоит из петель). На рис. 16 схематически изображен путь Марса за полгода, как он представляется земному наблюдателю (влияние вращения Земли вокруг своей оси здесь не отображено). Именно для описания петель в системе Птолемея использовались эпициклы.
в поезде, движущемся по прямому пути с постоянной скоростью. Пусть пассажир бросит из окна вагона тяжелый камень. По какому пути падает камень на землю?
По инерции камень продолжает движение с такой же скоростью, как и вагон, т. е. камень все время остается напротив окна вагона. В то же самое время он падает вниз. Человек, сидящий в поезде, скажет, что камень падает на землю по вертикальной прямой. Может ли то же самое сказать человек, стоящий у полотна железной дороги? Нет, не может. Он видит, что камень продолжает движение в направлении движения поезда, падая в то же время вниз. Выброшенный из окна вагона камень летит, как и брошенное горизонтально тело, по параболе. Траектория камня будет параболой, так будет утверждать человек, стоящий у полотна.
Не имеет смысла спрашивать, какова «действительная» траектория камня — прямая или парабола. Траектория тела не абсолютное понятие, о траектории можно говорить только относительно заданного тела отсчета. В разных системах отсчета траектория будет иметь различный вид. В то время как в системе отсчета, связанной с движущимся поездом, траекторией камня является прямая, в системе отсчета, связанной с Землей, она оказывается параболой. Траектория, как и скорость,— понятие относительное. О форме траектории имеет смысл говорить только после того, как будет фиксирована система отсчета.
Можно привести множество примеров, демонстрирующих, что понятие траектории относительно. Так, например, орбита планеты Марс по отношению к Солнцу — эллипс, относительно же Земли орбита будет иметь гораздо более сложный вид (она состоит из петель). На рис. 16 схематически изображен путь Марса за полгода, как он представляется земному наблюдателю (влияние вращения Земли вокруг своей оси здесь не отображено). Именно для описания петель в системе Птолемея использовались эпициклы.
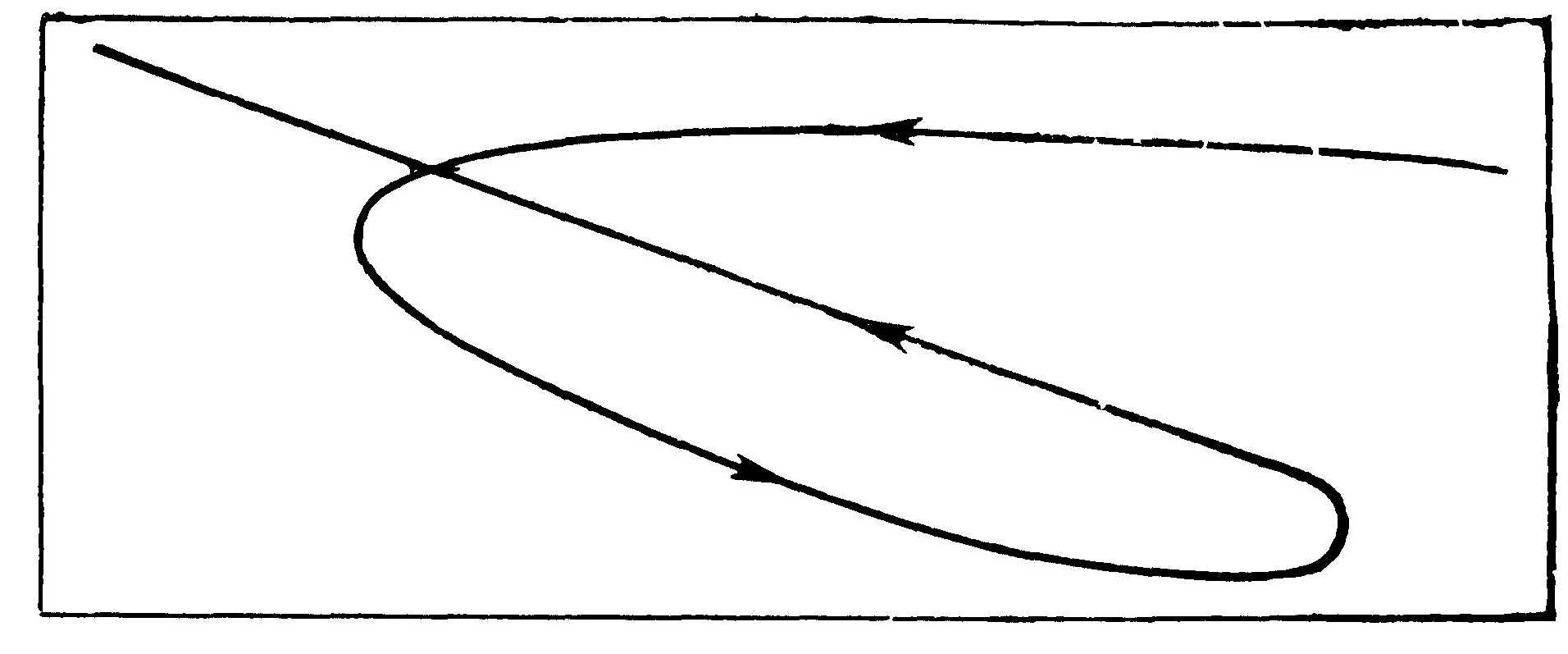
Рис. 16. Видимое движение Марса на небосводе
Рассмотрим другой пример. В земной системе отсчета у самой Земли траектория отсутствует (Земля неподвижна относительно себя), в то же время в системе Солнца траектория Земли будет эллипсом, как у Марса.
Две величины, характеризующие движение тела,— траектория и скорость — относительны. Возникает впечатление, что соответственно этому должно быть и два принципа относительности: принцип относительности скорости и принцип относительности траектория. В действительности получается совсем не так. Вычисления показывают, что относительность траектории следует из относительности скорости. Тем самым для теории движения вполне достаточно только одного принципа относительности, а именно: классического принципа относительности, или принципа относительности скорости.
Две величины, характеризующие движение тела,— траектория и скорость — относительны. Возникает впечатление, что соответственно этому должно быть и два принципа относительности: принцип относительности скорости и принцип относительности траектория. В действительности получается совсем не так. Вычисления показывают, что относительность траектории следует из относительности скорости. Тем самым для теории движения вполне достаточно только одного принципа относительности, а именно: классического принципа относительности, или принципа относительности скорости.