Под энергией тела физики понимают запас работы, за­ключенный в теле. Работа в физике — это любое преодо­ление воздействия. Когда мяч разбивает окно, он соверша­ет работу. У летевшего мяча был запас энергии, часть ко­торой была затрачена на то, чтобы разбить стекло.
Классическая механика утверждает, что энергия сво­бодного тела обусловлена только его движением, это так называемая кинетическая энергия. Если тело с массой то движется со скоростью v, то его кинетическая энергия Е выражается в классической физике известной формулой
E=m_0*v²/2    (6)
(индексом нуль при m мы подчеркиваем, что масса не за­висит от скорости движения тела).

Под энергией тела физики понимают запас работы, за­ключенный в теле. Работа в физике — это любое преодо­ление воздействия. Когда мяч разбивает окно, он соверша­ет работу. У летевшего мяча был запас энергии, часть ко­торой была затрачена на то, чтобы разбить стекло.
Классическая механика утверждает, что энергия сво­бодного тела обусловлена только его движением, это так называемая кинетическая энергия. Если тело с массой то движется со скоростью v, то его кинетическая энергия Е выражается в классической физике известной формулой
E=m_0*v²/2    (6)
(индексом нуль при m мы подчеркиваем, что масса не за­висит от скорости движения тела).
Кинетическая энергия определяется скоростью тела. Скорость же, как известно, в свою очередь, зависит от си­стемы отсчета. Отсюда видно, что кинетическая энергия тела зависит от системы отсчета. В каждой системе отсче­та энергия имеет свое значение. Следовательно, энергия даже в классической механике является относительной ве­личиной.
С относительностью кинетической энергии мы часто встречаемся в повседневной жизни. Например, кинетиче­ская энергия маленького камня, брошенного в воздух, не­велика относительно Земли. Относительно же быстро мча­щейся автомашины кинетическая энергия этого камня уже достаточна для того, чтобы разбить ветровое стекло автомашины и даже поранить водителя. Известны случаи, когда вылетевшие из-под колес передней автомашины ка­мушки причиняли серьезные повреждения движущейся следом автомашине.
Что говорит теория относительности об энергии свобод­ного тела? Выше мы видели, что поправки, которые тео­рия относительности вносит в классическую механику, при малых скоростях совершенно незначительны, только для больших скоростей они становились существенными. Ка­залось бы, можно ожидать, что так же будет обстоять дело и с энергией: при малых скоростях формула для энергии в теории относительности будет совпадать с формулой (6); при больших скоростях будут наблюдаться отличия. Од­нако эти ожидания в действительности не оправдываются.
Если масса покоя тела m₀ и скорость ѵ, то энергия его в теории относительности выражается формулой

(индексом r у Е мы подчеркиваем, что здесь мы имеем де­ло с выведенным в теории относительности релятивист­ским выражением для энергии).
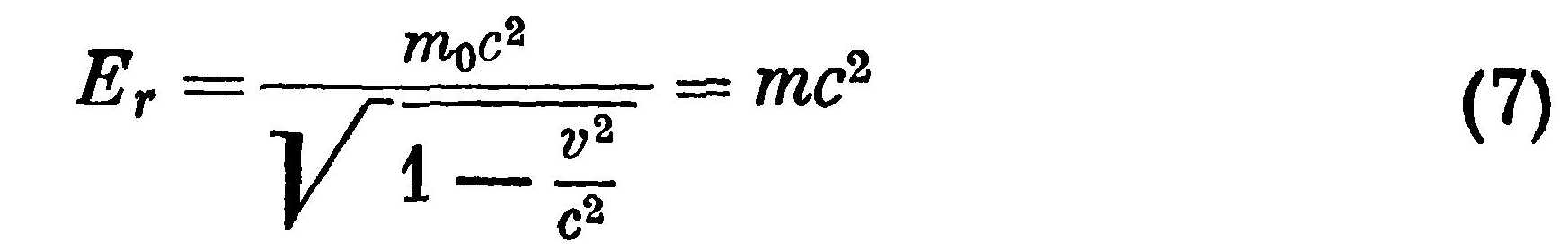
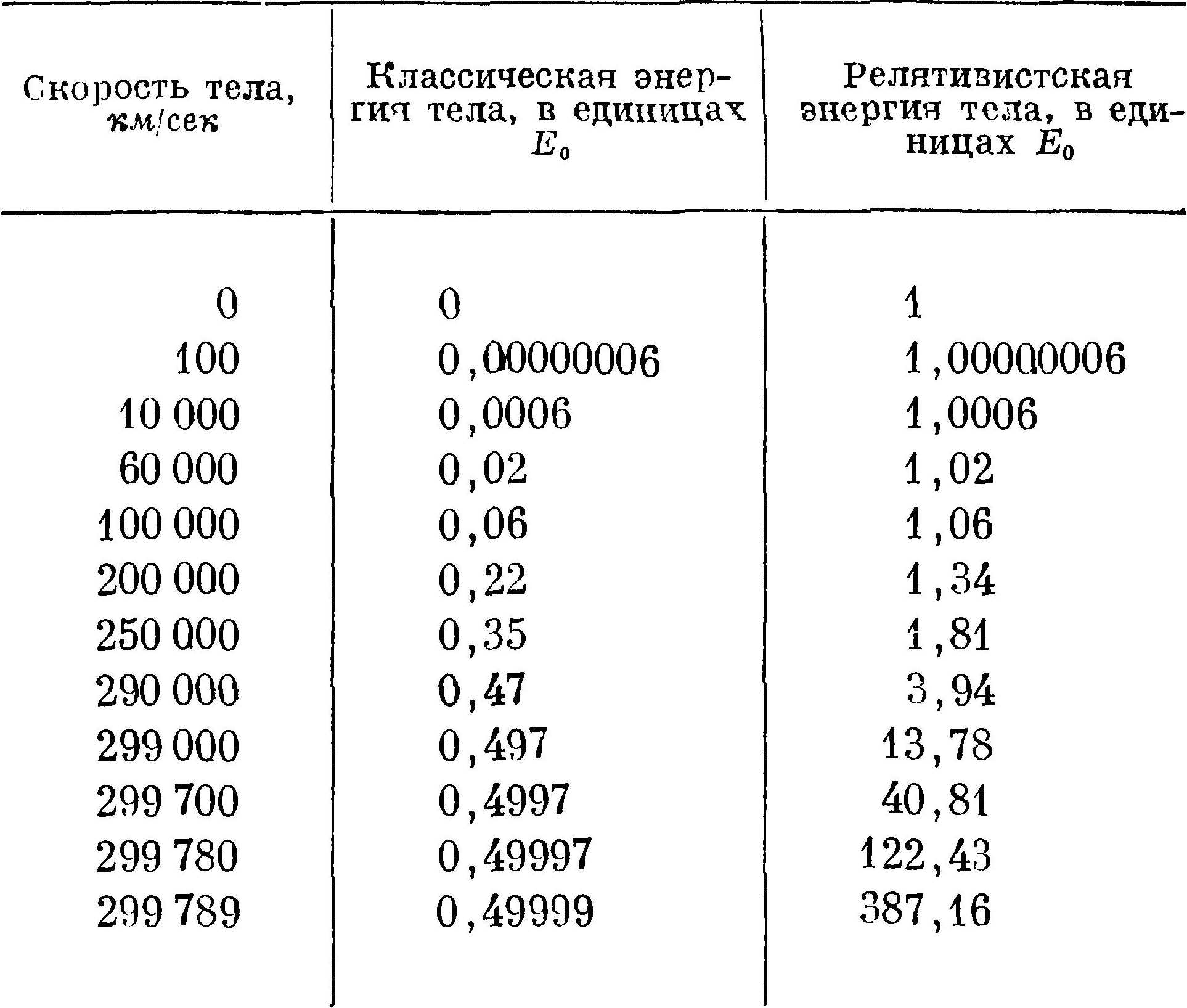
Формула (7) значительно отличается от формулы (6) даже для покоящегося тела. Если скорость ѵ равна нулю, формула классической механики дает кинетическую энер­гию, равную нулю. В релятивистском выражении при ѵ=0 энергия равна не нулю, а m₀с². Релятивистскую энергию покоящегося тела назовем энергией покоя и обозначим че­рез Е₀. (Сравнение классической кинетической энергии те­ла с релятивистской приведено в табл. 7.)
E₀ = m₀с²    (8)

 

Таблица  7
Сравнение классической кинетической энергии тела с релятивистской энергией

 

 

Простые расчеты показывает, что энергия покоя очень велика даже для малых тел. Так, например, для тела, маc­са покоя которого равна 1 г, энергия покоя составляет 99 180 000 миллионов килограммометров. За счет этой энергии можно было бы поднять груз весом в 918 000 т на высоту 10 км. Такой колоссальный запас энергии со­держит в себе 1 г вещества — на это указывает нам тео­рия относительности. Классическая же физика не мо­жет сказать ничего о существовании подобной энергии. В табл. 7 за единицу энергии выбрана энергия покоя Е₀. Если скорость тела приближается к скорости света, классическая кинетическая энергия, вычисленная соглас­но формуле классической физики, становится равной по­ловине энергии покоя, т. е. половине той энергии, которую согласно теории относительности имеет уже покоящееся тело.

 

Рис. 42. Сравнение классической энергии тела (сплошная линия) и релятивистской энергии (пунктирная линия), E₀  обозначает энер­гию покоя тела

 

По теории относительности в случае, когда скорость тела очень  близка к  скорости   света,   энергия   тела становится неограниченно большой. Другими словами: ре­лятивистская энергия тела может стать сколь угодно боль­шой, если только скорость тела достаточно близка к ско­рости света. На основе данных табл. 7 составлены графики рис. 42.
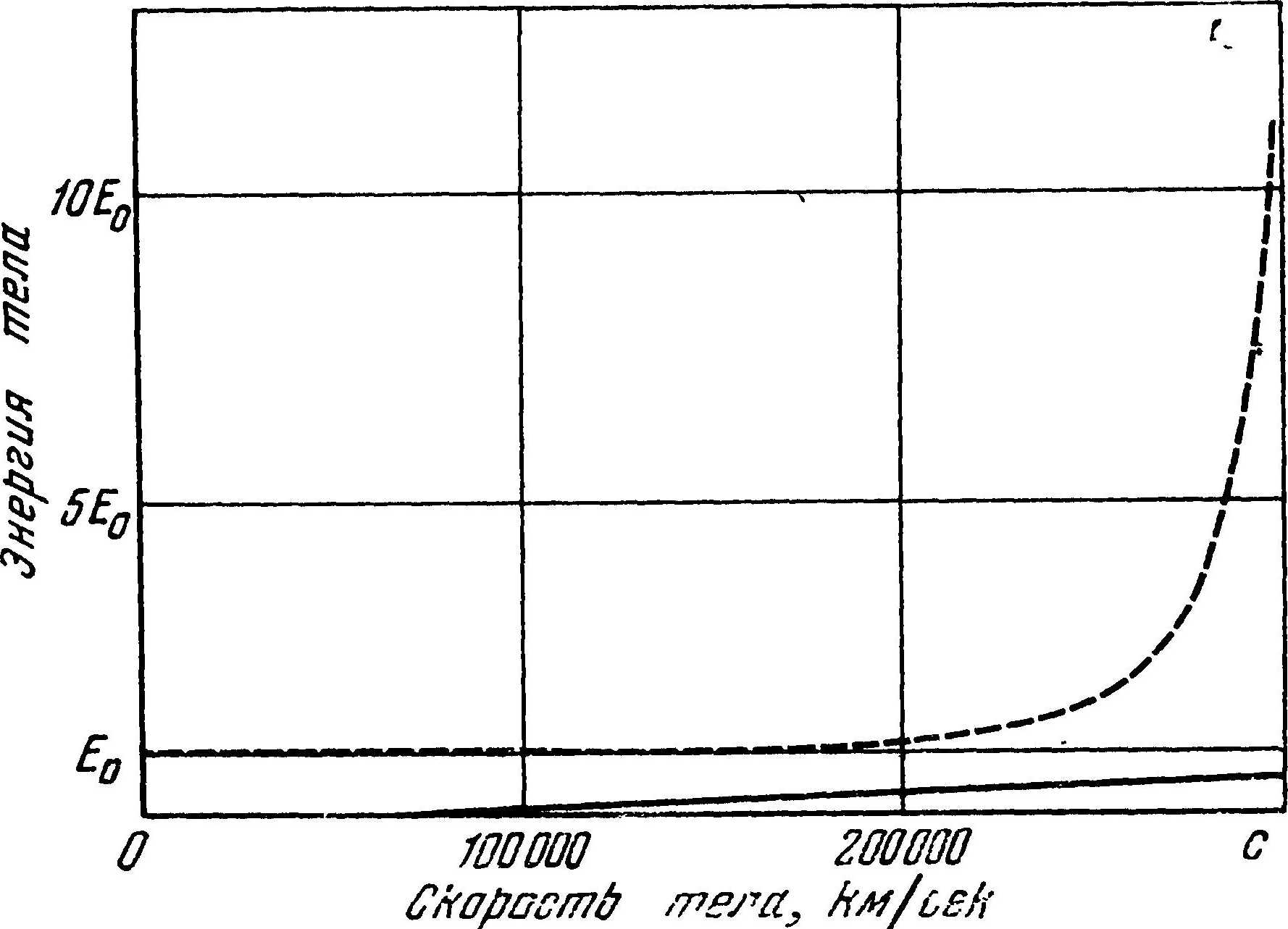
Выражение для релятивистской энергии может быть записа­но в виде бесконечного ряда. Первые члены этого ряда таковы:

 

Если скорость v мала по сравнению со скоростью света, то все члены, начиная с третьего, будут очень малы (в знаменателе сто­ит скорость света), и мы можем их не учитывать. Релятивистская энергия тела, движущегося с малой скоростью, достаточно точно выражается формулой

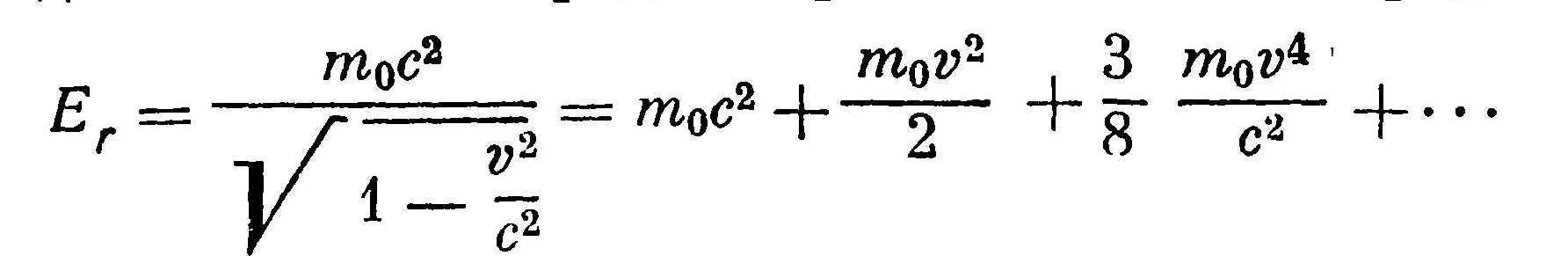
где m₀c² — энергия покоя.
Таким образом, энергия тела равняется сумме энергии покоя и классической кинетической энергии.
В классической физике нас интересует только разность энер­гий. Вычитая, например, начальную энергию тела, участвующего в каком-либо процессе, из его конечной энергии, получаем изме­нение энергии в данном процессе. Если масса покоя тела т0 не изменяется в процессе, то при образовании разностей энергий первый член в выражении энергии выпадает. Описывая такие процессы, можно уже с самого начала не записывать этот член. Отсюда видно, что классическое (выражение для энергии можно использовать при энергетических вычислениях только тогда, ког­да выполняются два условия:
а)    скорость рассматриваемого тела мала по сравнению со скоростью света;
б)    массы покоя участвующих в исследуемом процессе тел не изменяются.
Если одно из этих условий не выполнено, то при вычисле­ниях необходимо пользоваться релятивистским выражением энер­гии (7).