Еще раз об Ахиллесе и черепахе. Вернемся к апории Зенона, в которой он пытался доказать, что быстроногий Ахиллес не способен догнать черепаху. На этот раз для разрешения апории воспользуемся принципом относительности.
Прежде мы изучали движение Ахиллеса и черепахи относительно Земли, т. е. в системе отсчета, связанной с Землей. Рассмотрим теперь эту задачу в системе отсчета, связанной с черепахой. Классический принцип относительности утверждает, что обе системы отсчета равноправны. Результат, следовательно, не должен зависеть от системы отсчета.
Использование системы отсчета, связанной с черепахой, означает, что теперь мы все скорости измеряем относительно черепахи. Скорость Ахиллеса по отношению к Земле — V, скорость черепахи — v. Скорость Ахиллеса относительно черепахи, следовательно, V—ѵ. Скорость же черепахи относительно ее самой, разумеется, равна нулю, т. е. в новой системе отсчета черепаха будет просто неподвижным телом, которое нужно достичь Ахиллесу, бегущему со скоростью V—v. После перехода к системе отсчета, связанной с черепахой, мы оказываемся перед проблемой из апории «Дихотомия»: нужно пройти расстояние s (первоначальное расстояние между черепахой и Ахиллесом) со скоростью V—ѵ.
Еще раз об Ахиллесе и черепахе. Вернемся к апории Зенона, в которой он пытался доказать, что быстроногий Ахиллес не способен догнать черепаху. На этот раз для разрешения апории воспользуемся принципом относительности.
Прежде мы изучали движение Ахиллеса и черепахи относительно Земли, т. е. в системе отсчета, связанной с Землей. Рассмотрим теперь эту задачу в системе отсчета, связанной с черепахой. Классический принцип относительности утверждает, что обе системы отсчета равноправны. Результат, следовательно, не должен зависеть от системы отсчета.
Использование системы отсчета, связанной с черепахой, означает, что теперь мы все скорости измеряем относительно черепахи. Скорость Ахиллеса по отношению к Земле — V, скорость черепахи — v. Скорость Ахиллеса относительно черепахи, следовательно, V—ѵ. Скорость же черепахи относительно ее самой, разумеется, равна нулю, т. е. в новой системе отсчета черепаха будет просто неподвижным телом, которое нужно достичь Ахиллесу, бегущему со скоростью V—v. После перехода к системе отсчета, связанной с черепахой, мы оказываемся перед проблемой из апории «Дихотомия»: нужно пройти расстояние s (первоначальное расстояние между черепахой и Ахиллесом) со скоростью V—ѵ. Очевидно, для этого необходимо время
Получим точно тот же результат, что и прежде.
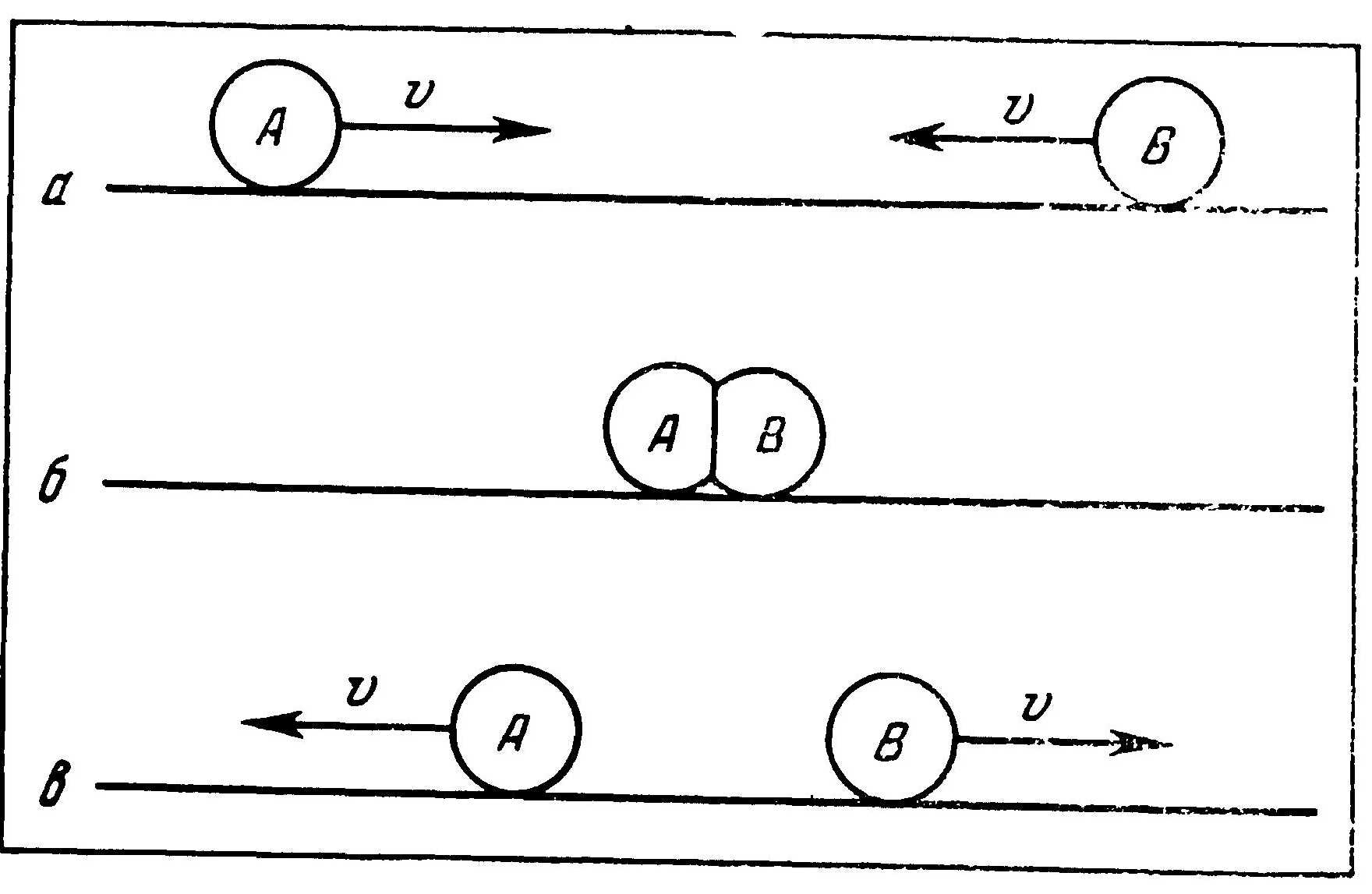
Законы упругих столкновений. Два шарика с одинаковыми радиусами и с равными массами сближаются п і прямой, каждый со скоростью ѵ относительно Земли (рис. 14, а). Столкнувшись, оба шарика деформируются и останавливаются (рис. 14, б). Если шарики сделаны из неупругого материала, этим все и кончается. У упругих же шариков вдавленные поверхности напряжены наподобие пружины. Как только движение шариков прекращается, они тотчас начинают восстанавливать свою прежнюю форму. Деформированные поверхности выпрямляются, и (если шарики абсолютно упруги) они отскакивают друг от друга с той же самой скоростью, с какой они сближались. После столкновения оба шарика катятся со скоростью ѵ в обратном направлении (рис. 14, в).
Так происходит столкновение двух упругих шариков с равными массами. Именно так сталкиваются, например, два бильярдных шара.
А что произойдет после столкновения двух одинаковых шариков с разными скоростями? Голландский ученый Гюйгенс еще в XVII в. показал, что с помощью принципа относительности подобный вопрос разрешается просто. Рассмотрим, например, такую задачу.
Приступая к решению этой задачи, Гюйгенс писал: «Когда пассажир некоторого корабля, движущегося с постоянной скоростью, приводит к соударению два равных шара с равными по отношению к нему и частям корабля скоростями, то они должны отскочить с равными же, по отношению к нему, скоростями, точно так же, как это имеет место для стоящего на берегу человека». Тем самым Гюйгенс учитывал принцип относительности: столкновение двух шаров на корабле, плывущем равномерной прямолинейно, происходит так же, как и на берегу. Этот принцип дает ключ для решения задачи.
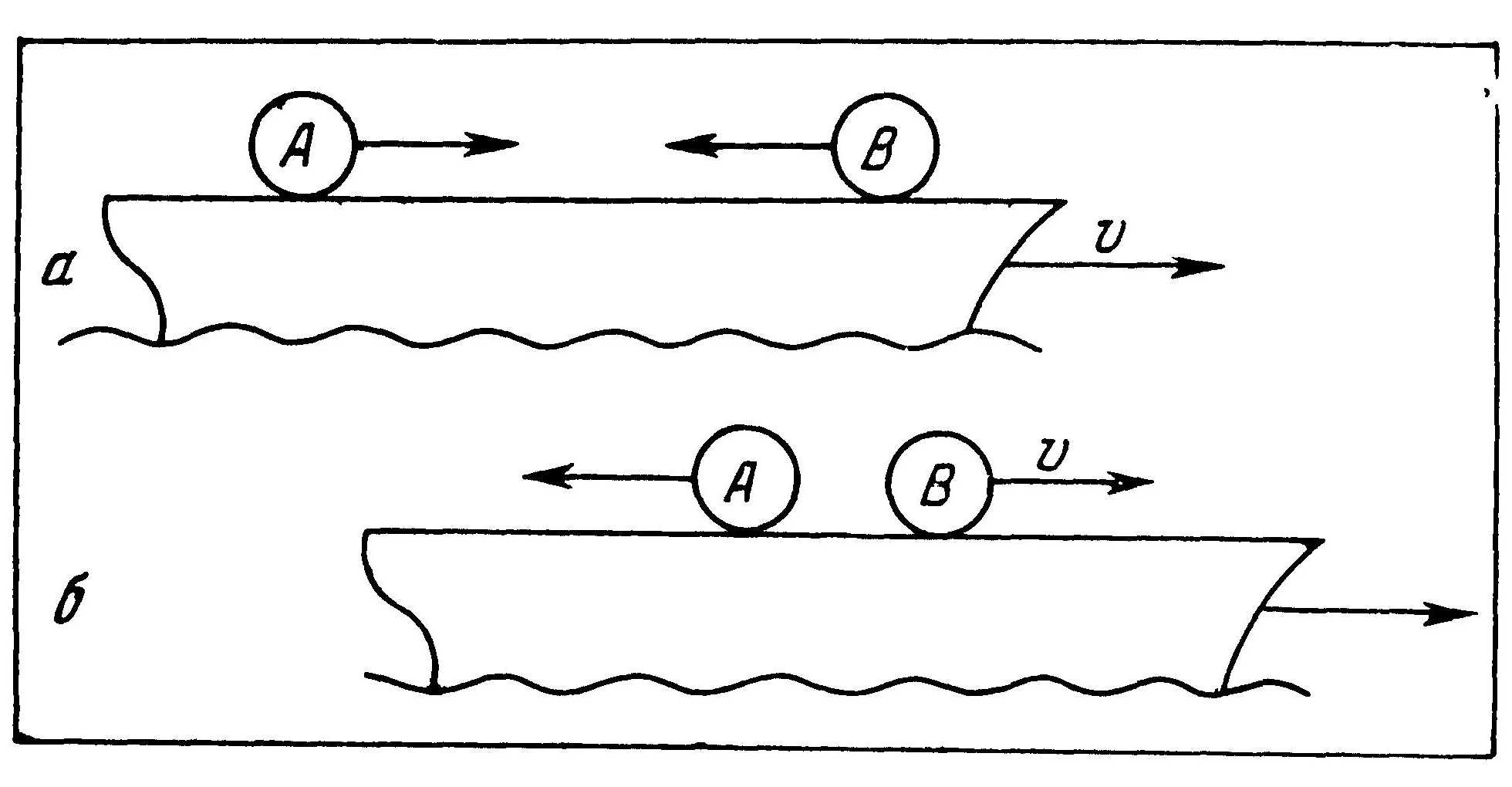
Стоящий на берегу наблюдатель увидит это же самое соударение иначе: до удара шар В совсем не движется относительно берега (насколько корабль уходит вперед, настолько же шар откатывается назад), тогда как шар А движется со скоростью 2ѵ по направлению движения корабля. Такими и были исходные данные нашей задачи. Следовательно, из рис. 15, б, на котором изображено движение шаров после удара, можно усмотреть решение задачи. Для этого нужно только определить, как шары движутся относительно берега. Очевидно, что после соударения шар А становится неподвижным по отношению к земной поверхности, а шар В начнет двигаться со скоростью 2ѵ направо. Это и будет решением задачи. Шар B, который перед соударением находился в покое, покатится со скоростью 2ѵ; двигавшийся же раньше шар А остановится. Двигавшийся шар передал при ударе всю
свою скорость (точнее весь свой импульс) покоившемуся, и сам остановился.
По аналогии с предыдущим читатель может выяснить характер упругих столкновении для одинаковых шаров, обладающих различными скоростями. При этом он легко установит общий закон: при упругом (центральном) соударении шары с равными массами обмениваются импульсами.