В главе, посвященной специальной теории относительности, мы видели, что конкретный вид электромагнитного поля зависит от системы отсчета, в которой это поле описывается. В одной системе отсчета поле имеет один вид, в другой — иной. Однако для электромагнитного поля характерна одна существенная черта: если электромагнитное поле имеется в некоторой заданной системе отсчета, то невозможно найти другую систему отсчета, в которой бы это поле отсутствовало. Электромагнитное поле нельзя устранить с помощью движения. Гравитационное поле обличается от электромагнитного главным образом именно этим свойством. Величина напряженности гравитационного ноля зависит от системы отсчета, в которой мы описываем ноле. Однако в противоположность электромагнитному нолю здесь всегда можно найти такую систему отсчета, в которой гравитационное поле в данной точке пространства равно нулю. Именно это и подразумевается в принципе эквивалентности, когда говорится об эквивалентности гравитационного поля и поля относительного ускорения. О принципе эквивалентности всегда говорится в связи с общей теорией относительности. В действительности принцип эквивалентности следует уже из закона свободного падения, открытого Галилеем, и относится по своему содержанию к классической физике. Значение принципа эквивалентности состоит не только в том, что он позволяет лучше понять сущность гравитационного поля, но у него есть и определенное методическое значение. Использование этого принципа позволяет уяснить некоторые вопросы и логически просто объяснить ряд явлений природы. Примерами могут служить уже рассмотренные проблемы, связанные с поведением силы тяжести в космическом полете. Поясним теперь, как использовать принцип эквивалентности для объяснения возникновения приливов и отливов.
В главе, посвященной специальной теории относительности, мы видели, что конкретный вид электромагнитного поля зависит от системы отсчета, в которой это поле описывается. В одной системе отсчета поле имеет один вид, в другой — иной. Однако для электромагнитного поля характерна одна существенная черта: если электромагнитное поле имеется в некоторой заданной системе отсчета, то невозможно найти другую систему отсчета, в которой бы это поле отсутствовало. Электромагнитное поле нельзя устранить с помощью движения. Гравитационное поле обличается от электромагнитного главным образом именно этим свойством. Величина напряженности гравитационного ноля зависит от системы отсчета, в которой мы описываем ноле. Однако в противоположность электромагнитному нолю здесь всегда можно найти такую систему отсчета, в которой гравитационное поле в данной точке пространства равно нулю. Именно это и подразумевается в принципе эквивалентности, когда говорится об эквивалентности гравитационного поля и поля относительного ускорения. О принципе эквивалентности всегда говорится в связи с общей теорией относительности. В действительности принцип эквивалентности следует уже из закона свободного падения, открытого Галилеем, и относится по своему содержанию к классической физике. Значение принципа эквивалентности состоит не только в том, что он позволяет лучше понять сущность гравитационного поля, но у него есть и определенное методическое значение. Использование этого принципа позволяет уяснить некоторые вопросы и логически просто объяснить ряд явлений природы. Примерами могут служить уже рассмотренные проблемы, связанные с поведением силы тяжести в космическом полете. Поясним теперь, как использовать принцип эквивалентности для объяснения возникновения приливов и отливов.
Напомним закон движения в гравитационном поле: свободное тело в гравитационном поле движется естественно, т. е. так, что в месте его нахождения постороннее гравитационное поле отсутствует. Движение тела уничтожает постороннее гравитационное поле. Однако в точном соответствии с этим законом могут двигаться маленькие, практически «точечные» тела. Для больших тел положение сложнее.
Пусть в гравитационном поле движется тело больших размеров, т. е. такое тело, в объеме которого гравитационное поле заметно меняется. Вообще говоря, в этом случае напряженность постороннего гравитационного поля в каждой точке тела будет различной, если само тело твердое и движется как единое целое (и не вращается), т. е. все точки тела будут двигаться с одним и тем же ускорением. Поэтому движение тела уничтожает повсюду одинаковую часть внешнего поля. Полностью уничтожить внешнее поле во всех точках тела невозможно. Тело больших размеров в гравитационном поле может двигаться лишь так, что поле можно полностью аннулировать только в одной его точке. Во всех остальных точках будет оставаться часть постороннего поля или же ускоренное движение будет порождать там дополнительное гравитационное ноле. Вычисления показывают, что такой точкой тела, в которой можно полностью аннулировать постороннее гравитационное поле, является центр масс. Таким образом, закон движения большого тела в гравитационном поле можно сформулировать следующим образом: большое тело движется в гравитационном поле так, что уничтожается постороннее гравитационное поле в его центре масс.
Напомним закон движения в гравитационном поле: свободное тело в гравитационном поле движется естественно, т. е. так, что в месте его нахождения постороннее гравитационное поле отсутствует. Движение тела уничтожает постороннее гравитационное поле. Однако в точном соответствии с этим законом могут двигаться маленькие, практически «точечные» тела. Для больших тел положение сложнее.
Пусть в гравитационном поле движется тело больших размеров, т. е. такое тело, в объеме которого гравитационное поле заметно меняется. Вообще говоря, в этом случае напряженность постороннего гравитационного поля в каждой точке тела будет различной, если само тело твердое и движется как единое целое (и не вращается), т. е. все точки тела будут двигаться с одним и тем же ускорением. Поэтому движение тела уничтожает повсюду одинаковую часть внешнего поля. Полностью уничтожить внешнее поле во всех точках тела невозможно. Тело больших размеров в гравитационном поле может двигаться лишь так, что поле можно полностью аннулировать только в одной его точке. Во всех остальных точках будет оставаться часть постороннего поля или же ускоренное движение будет порождать там дополнительное гравитационное ноле. Вычисления показывают, что такой точкой тела, в которой можно полностью аннулировать постороннее гравитационное поле, является центр масс. Таким образом, закон движения большого тела в гравитационном поле можно сформулировать следующим образом: большое тело движется в гравитационном поле так, что уничтожается постороннее гравитационное поле в его центре масс.
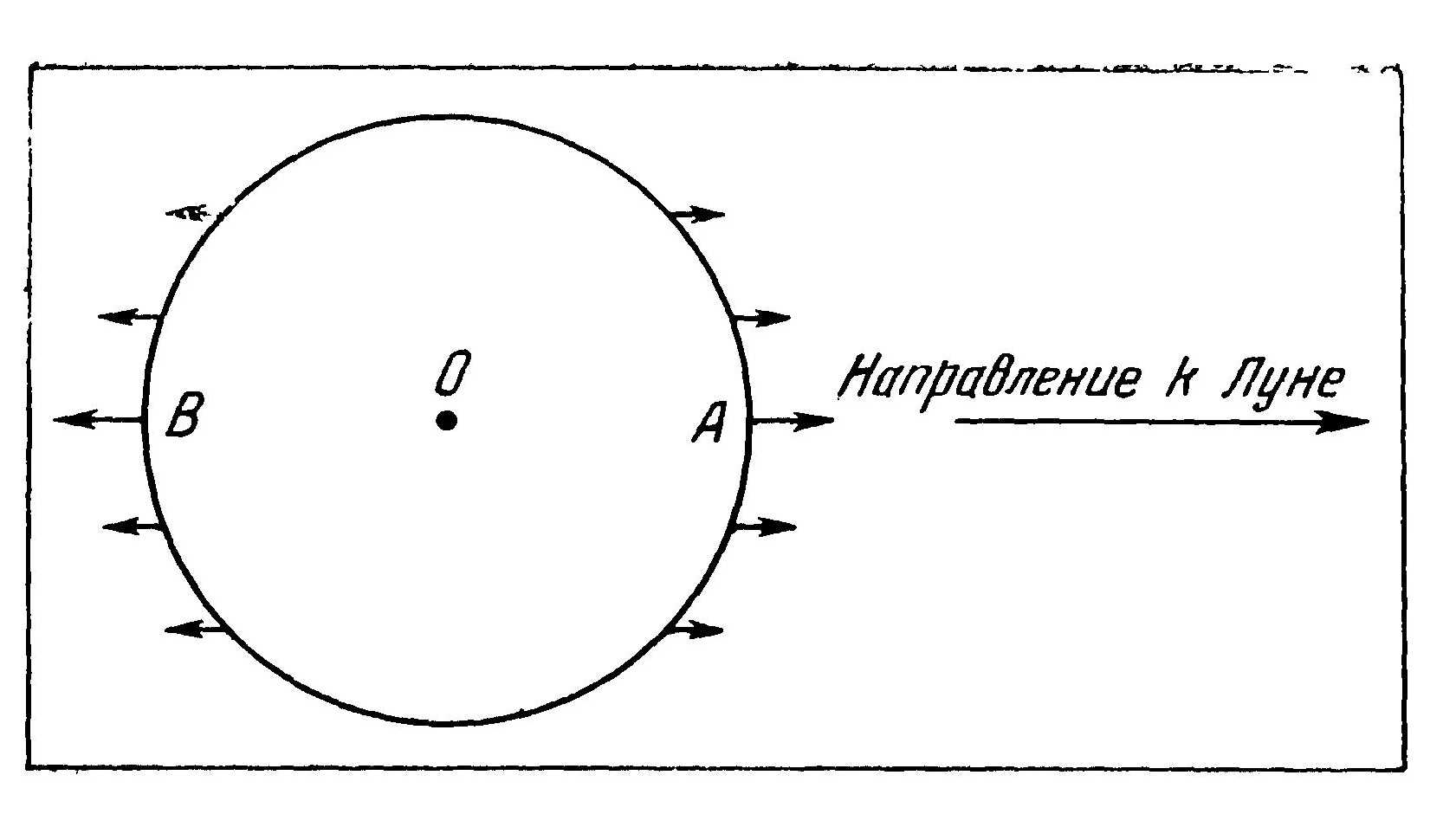
Рис. 49. Гравитационное поле Луны в системе отсчета, связанной с Землей
К примеру, Земля движется в гравитационном поле Луны так, что в центре Земли это поле равно нулю. Ускоренное движение Земли уничтожает гравитационное поле Луны (а также и все другие посторонние гравитационные поля) в центре Земли.
В той части земного шара (рис 49), которая обращена к Луне (точкаА),лунное гравитационное поле сильнее,чем в центре земного шара О. На противоположной стороне земного шара (точка В) гравитационное поле Луны слабее, чем в центре О. Поэтому в то время, как движение Земли уничтожает гравитационное поле в центре Земли, на ее стороне, обращенной к Луне, остается нескомпенсированным слабое поле. Под действием этого поля в океане образуется прилив. На поверхности же, обращенной в противоположную сторону, движение Земли не только компенсирует лунное гравитационное поле, но и создает избыток в виде силы, направленной от Луны. Под влиянием этой силы также образуется приливная волна.
На рисунке изображена стрелками та часть гравитационного поля Луны, которое обнаруживает находящийся на Земле наблюдатель. Это гравитационное поле Луны в системе отсчета, связанной с Землей. В системе же отсчета Луны ее собственное гравитационное поле определяется обычным законом гравитации, т. е. оно сильнее всего в непосредственной окрестности Луны и уменьшается обратно пропорционально квадрату расстояния. Это еще раз показывает, как сильно зависит вид поля от системы отсчета, в которой оно описывается. Если нас интересует воздействие гравитационного поля Луны на земные тела, мы всегда должны рассматривать это поле таким, каким оно является в системе отсчета Земли. И возникновение приливов и отливов также следует описывать в этой системе отсчета. Объяснять возникновение приливов и отливов на Земле гравитационным полем Луны в том виде, какой оно имеет в системе отсчета, связанной с Луной, как это, к сожалению, часто делают в учебниках для средней школы, нельзя.
Как видим, принцип эквивалентности позволяет дать очень простое и ясное описание приливных явлений. Из приведенного объяснения вытекает несколько простых следствий.
Напряженность поля, обусловливающего приливы и отливы, не зависит от напряженности постороннего гравитационного поля в месте, где находится планета. Оно зависит только от того, насколько изменяется напряженность постороннего гравитационного поля в объеме планеты. Например, гравитационное поле Солнца в окрестности Земли в 180 раз сильнее поля Луны. Несмотря на это, как известно, солнечные приливы значительно слабее лунных. Причина состоит в том, что изменение гравитационного поля Солнца в объеме Земли в 2,2 раза меньше изменения гравитационного поля Луны.
Из предыдущего также следует, что гравитационная сила, порождающая приливы и отливы, тем больше, чем больше поперечник планеты. Если при сохранении всех прочих условий поперечник Земли стал бы больше, то и приливная волна была бы выше.
В той части земного шара (рис 49), которая обращена к Луне (точкаА),лунное гравитационное поле сильнее,чем в центре земного шара О. На противоположной стороне земного шара (точка В) гравитационное поле Луны слабее, чем в центре О. Поэтому в то время, как движение Земли уничтожает гравитационное поле в центре Земли, на ее стороне, обращенной к Луне, остается нескомпенсированным слабое поле. Под действием этого поля в океане образуется прилив. На поверхности же, обращенной в противоположную сторону, движение Земли не только компенсирует лунное гравитационное поле, но и создает избыток в виде силы, направленной от Луны. Под влиянием этой силы также образуется приливная волна.
На рисунке изображена стрелками та часть гравитационного поля Луны, которое обнаруживает находящийся на Земле наблюдатель. Это гравитационное поле Луны в системе отсчета, связанной с Землей. В системе же отсчета Луны ее собственное гравитационное поле определяется обычным законом гравитации, т. е. оно сильнее всего в непосредственной окрестности Луны и уменьшается обратно пропорционально квадрату расстояния. Это еще раз показывает, как сильно зависит вид поля от системы отсчета, в которой оно описывается. Если нас интересует воздействие гравитационного поля Луны на земные тела, мы всегда должны рассматривать это поле таким, каким оно является в системе отсчета Земли. И возникновение приливов и отливов также следует описывать в этой системе отсчета. Объяснять возникновение приливов и отливов на Земле гравитационным полем Луны в том виде, какой оно имеет в системе отсчета, связанной с Луной, как это, к сожалению, часто делают в учебниках для средней школы, нельзя.
Как видим, принцип эквивалентности позволяет дать очень простое и ясное описание приливных явлений. Из приведенного объяснения вытекает несколько простых следствий.
Напряженность поля, обусловливающего приливы и отливы, не зависит от напряженности постороннего гравитационного поля в месте, где находится планета. Оно зависит только от того, насколько изменяется напряженность постороннего гравитационного поля в объеме планеты. Например, гравитационное поле Солнца в окрестности Земли в 180 раз сильнее поля Луны. Несмотря на это, как известно, солнечные приливы значительно слабее лунных. Причина состоит в том, что изменение гравитационного поля Солнца в объеме Земли в 2,2 раза меньше изменения гравитационного поля Луны.
Из предыдущего также следует, что гравитационная сила, порождающая приливы и отливы, тем больше, чем больше поперечник планеты. Если при сохранении всех прочих условий поперечник Земли стал бы больше, то и приливная волна была бы выше.