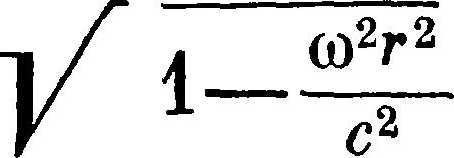Вернемся снова к вопросу о геометрии мирового пространства. Можем ли мы описывать геометрические фигуры, построенные (мысленно) в мировом пространстве с помощью геометрии Евклида, или здесь необходимо применять геометрию Лобачевского либо Римана? Евклидова геометрия нам хорошо известна из школьного курса. В этой геометрии утверждается, например, что сумма внутренних углов треугольника равна 180°, а длина окружности равна 2Пr, где r — радиус этой окружности. Геометрия Римана и Лобачевского не содержит таких утверждений. Казалось бы, выбор геометрии в принципе не сложен. Для этого нужно «только» измерить геометрические фигуры в космическом пространстве и установить, отвечают ли результаты измерений евклидовой геометрии или нет. Если бы можно было, например, построить окружность гигантских (космических) размеров с радиусом R и измерить ее длину, то сразу же можно бы сделать выводы о геометрических свойствах пространства. Если бы длина такой окружности оказалась равной 2ПR, то мы смогли бы утверждать, что в мировом пространстве справедлива геометрия Евклида. Если бы длина окружности оказалась больше или меньше 2ПR, то мы смогли бы сделать заключение, что в мировом пространстве справедлива геометрия, отличная от евклидовой. Остановимся на проблеме измерения длины окружности.
Вернемся снова к вопросу о геометрии мирового пространства. Можем ли мы описывать геометрические фигуры, построенные (мысленно) в мировом пространстве с помощью геометрии Евклида, или здесь необходимо применять геометрию Лобачевского либо Римана? Евклидова геометрия нам хорошо известна из школьного курса. В этой геометрии утверждается, например, что сумма внутренних углов треугольника равна 180°, а длина окружности равна 2Пr, где r — радиус этой окружности. Геометрия Римана и Лобачевского не содержит таких утверждений. Казалось бы, выбор геометрии в принципе не сложен. Для этого нужно «только» измерить геометрические фигуры в космическом пространстве и установить, отвечают ли результаты измерений евклидовой геометрии или нет. Если бы можно было, например, построить окружность гигантских (космических) размеров с радиусом R и измерить ее длину, то сразу же можно бы сделать выводы о геометрических свойствах пространства. Если бы длина такой окружности оказалась равной 2ПR, то мы смогли бы утверждать, что в мировом пространстве справедлива геометрия Евклида. Если бы длина окружности оказалась больше или меньше 2ПR, то мы смогли бы сделать заключение, что в мировом пространстве справедлива геометрия, отличная от евклидовой. Остановимся на проблеме измерения длины окружности.
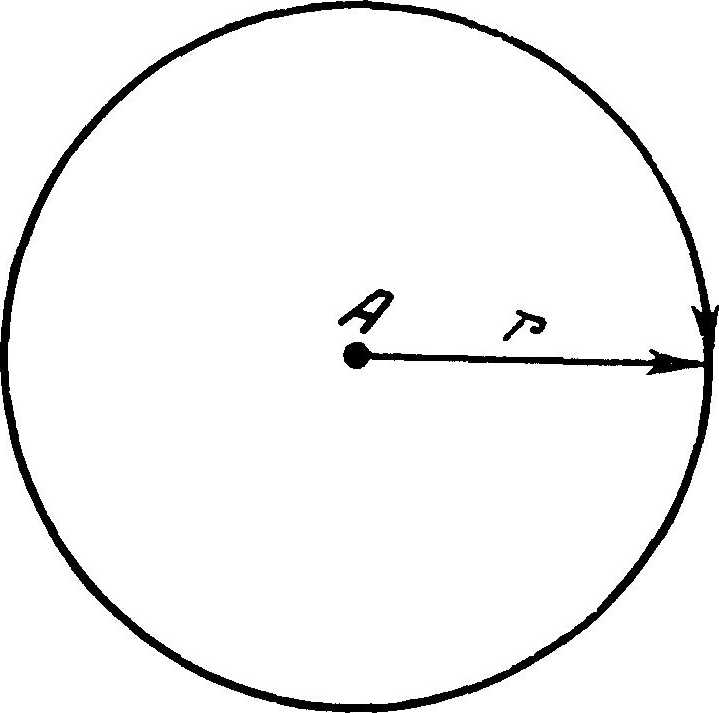
Рис. 50.
На рис. 50 изображена окружность радиуса r. Предположим, что эта окружность неподвижна относительно какой-то инерциальной системы. Пусть в центре А окружности находятся два наблюдателя: один из них неподвижен относительно окружности, а другой вращается с угловой скоростью со. Если мы спросим первого наблюдателя, то он без колебаний скажет, что радиус окружности равен r, а длина ее составляет 2Пr. Как оценит длину окружности наблюдатель, который вращается с угловой скоростью w? По отношению к нему все точки окружности движутся со скоростью ѵ = wr. Так как каждый небольшой отрезок окружности длиной l движется с линейной скоростью wr, то, соглас но формуле (4), длина этого отрезка, измеренная им, будет равна
Каждый небольшой отрезок окружности будет сокращаться в
раз, значит, во столько же раз должна сократиться и вся окружность. Длина окружности для наблюдателя, который вращается, будет равна
В то же время длина радиуса окружности (перпендикулярного направлению вращения) не будет изменяться и останется равной r. Таким образом, для определения длины окружности по ее радиусу выводы евклидовой геометрии оказываются несправедливыми. По мнению наблюдателя, который вращается, евклидова геометрия непригодна для описания пространства, с его точки зрения пространство не является евклидовым.
Приведенное рассуждение весьма приближенно, но, несмотря на это, оно указывает на факт непригодности евклидовой геометрии в неинерциальных системах. С другой стороны, в предыдущих параграфах мы видели, что неинерци-альность системы отсчета проявляется в виде силы, которую мы в небольшой области пространства и в течение короткого промежутка времени не можем отличить от силы тяжести. Вместо того, чтобы говорить о неинерциальной системе отсчета, мы можем говорить об инерциальной системе, в которой действует сила тяжести. Отсюда следует, что существование в пространстве гравитационного поля обусловливает неевклидовость пространства. Чем сильнее гравитационное поле в рассматриваемой области пространства, тем больше геометрия этой области отличается от евклидовой.
В мировом пространстве имеется гравитационное поле, следовательно, оно не будет евклидовым. Пространство с геометрией, отличающейся от евклидовой, называется «искривленным пространством». Реальное мировое пространство искривлено. Как мы должны понимать это выражение?
В своей книге «Эволюция физики» А. Эйнштейн и Л. Инфельд иллюстрируют кривое пространство следующим рассуждением.
Каждый видел на киноэкране движущихся людей. Это двумерные люди, так как их размеры определяются только длиной и шириной; третье же измерение, которое имеется у настоящих людей, у них отсутствует. Предположим теперь, что эти двумерные люди, движущиеся на экране, действительно существуют: они ходят на экране, думают и изучают все окружающее. Пространство, где живут эти люди, — двумерный экран, вне которого они никоим образом не могут осуществлять наблюдений. Люди двумерного экрана не могут представить себе трехмерный мир. Эти люди знают, что такое кривые линии? — такие линии на экране есть, но они не могут представить искривленной поверхности. Осуществляя измерения различных геометрических образов, они будут убеждены, что в мире действуют именно такие геометрические законы, которые составляют предмет планиметрии. Другими словами, их пространство будет двумерным евклидовым пространством.
Пусть экран будет изготовлен из эластичного материала, так что мы можем его растягивать, превращая из плоскости в кривую поверхность. Воображаемые люди на экране такой деформации непосредственно не заметят, но различные их измерения покажут, что законы геометрии для них уже не будут законами обычной планиметрии. Так, например, сумма внутренних углов треугольника будет больше 180°. Двумерные люди могут с полным правом утверждать, что их мир больше не евклидов, потому что находящиеся в нем тела обладают иными? свойствами, чем образы евклидовой геометрии.
Если экран, на котором живут наши воображаемые люди, будет очень большим, то может случиться, что кривизна небольшого участка экрана практически не будет заметна (так, например, мы не считаем искривленным небольшой участок земной поверхности). Двумерные люди долгое время будут убеждены, что их мир плоский. Только по мере изучения исключительно больших участков «экрана» они смогут убедиться, что их мир все-таки искривлен. Однакоэта кривизна так мала, что при изучении небольших кусочков экрана она останется незамеченной.
Наше положение весьма сходно с тем, в котором находятся люди экрана. Разница состоит только в том, что мы сами и наше пространство не двумерны, а трехмерны. Как двумерные люди не могли наглядно представить кривизну своего пространства, так не можем сделать этого и? мы. Кривизна пространства выражается лишь в том, что построенные в нем геометрические фигуры нужно рассчитывать по законам неевклидовой геометрии, поскольку обычная евклидова геометрия дает результаты, не согласующиеся с действительностью.
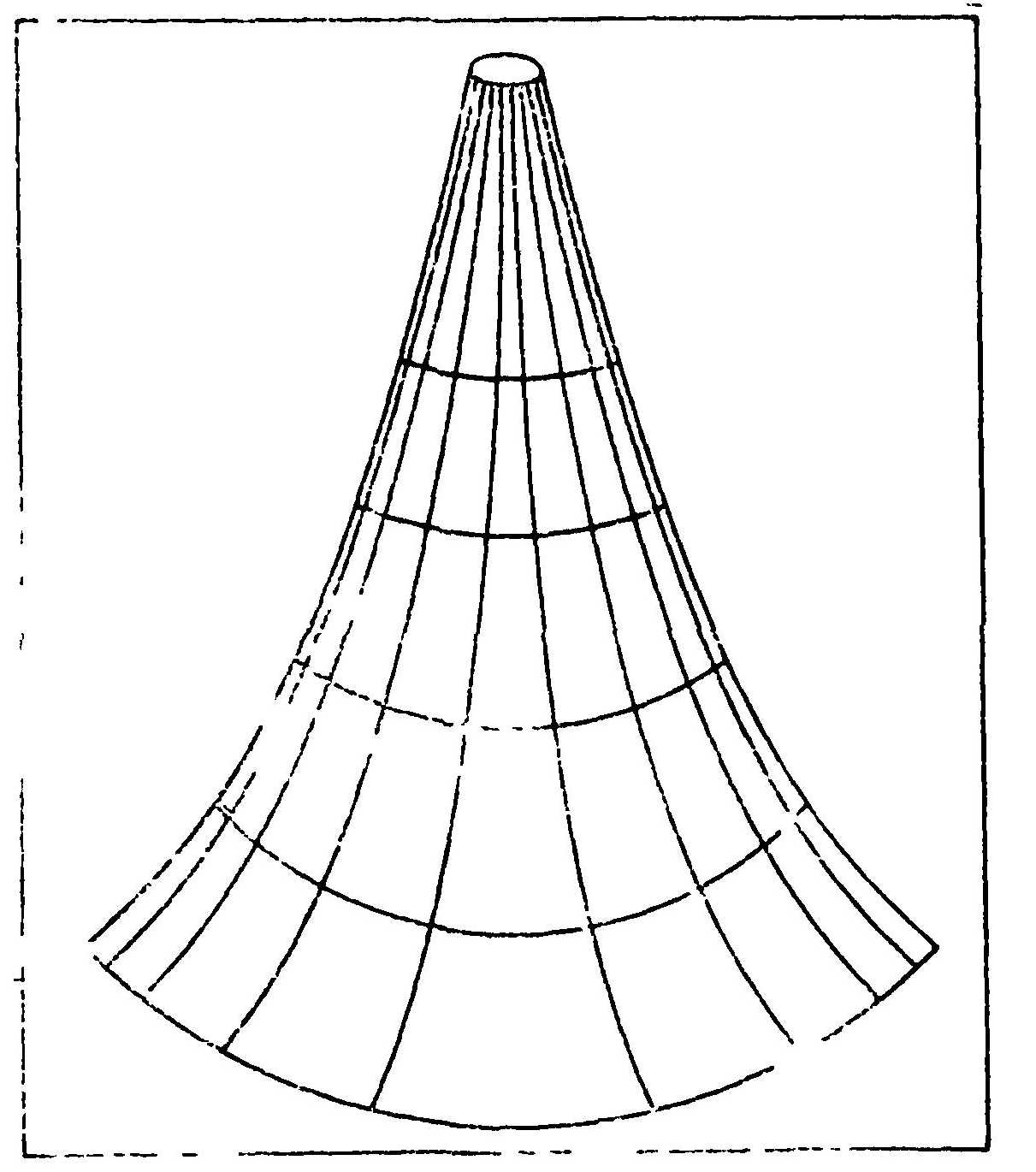
Рис. 51. Часть поверхности с отрицательной кривизной. Сумма внутренних углов треугольника, начерченного на такой поверхности, меньше 180°
Кривые поверхности можно характеризовать их кривизной. Математики показали, что можно пользоваться также и понятием кривизны пространства. Если кривизна пространства равна нулю, то мы имеем дело с пространством, в котором справедливы теоремы евклидовой геометрии. В этом случае говорят, что мы имеем дело с плоским пространством. Искривленные пространства делят на две группы: пространства с положительной и пространства с отрицательной кривизной (рис. 51). Каждое из них имеет свои особенности.
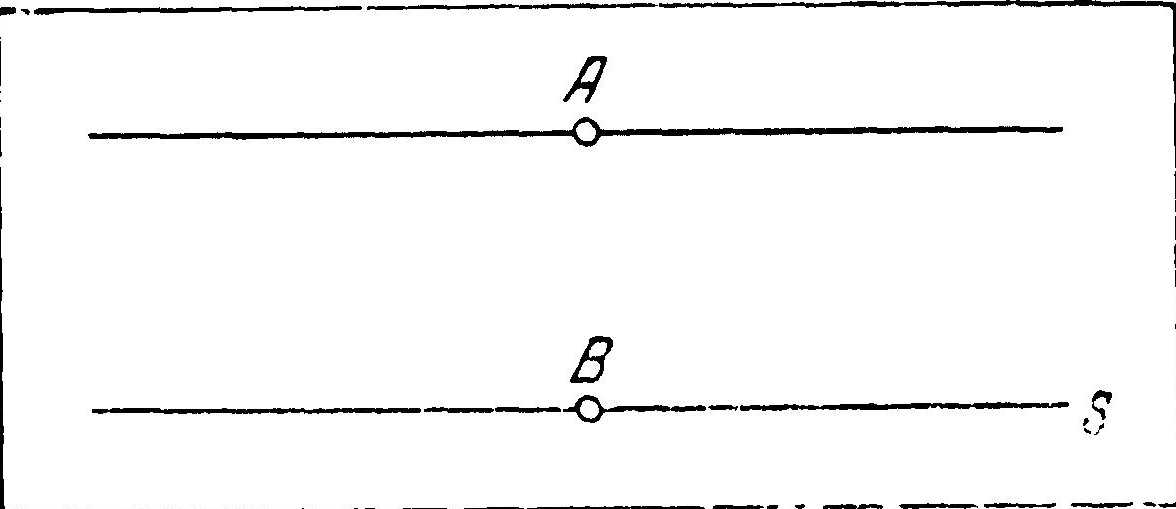
Рис. 52. Геометрия пространства нулевой кривизны. Через заданную точку А можно провести по отношению к прямой s только одну параллельную прямую
Из школьного курса геометрии мы знаем, например, аксиому: через точку А, іне лежащую на прямой s, можно провести одну и только одну прямую, которая, находясь в одной плоскости с прямой s, не пересекает ее (рис. 52). Для пространства с отрицательной кривизной существует совсем иная аксиома: через точку A, расположенную вне прямой s, можно провести по меньшей мере две прямые, которые лежат в одной плоскости с прямой s, но не пересекают последней (вслед за тем можно уже доказать, что в действительности таких прямых будет бесконечное множество). Это значит, что в пространстве с отрицательной кривизной через А можно провести бесконечное количество прямых, параллельных прямой s. Интересно отметить, что Я. Больяй, исходя именно из этой, так называемой аксиомы о параллельных прямых, построил свою неевклидову геометрию (рассуждения в теории Лобачевского были аналогичными).
Аксиому Евклида невозможно проверить практически: ведь мы не можем проследить бесконечные прямые на всем их протяжении. Больяй сделал предположение, что через точку А проходят по меньшей мере две различные прямые, обе параллельные данной прямой, и надеялся, что это приведет его к противоречиям в геометрических рассуждениях. Тогда евклидова аксиома была бы доказана (и тем самым превратилась бы уже в теорему). Но результат получился совершенно неожиданным. Больяй доказывал одну теорему за другой и нигде не встречал противоречия. И тогда он понял, что доказанные теоремы образуют новую, лишенную внутренних противоречий геометрическую систему, которая отличается от евклидовой геометрии. Так появилась геометрия пространства с отрицательной кривизной.
Аналогично может быть построена и геометрия пространства с положительной кривизной. Для этого рассмотренную аксиому нужно заменить следующей: каждая прямая, расположенная в одной плоскости с прямой s, пересекает последнюю. Это значит, что через точку А нельзя провести ни одной прямой, параллельной s.
