Апории Зенона были предметом размышления мате­матиков и философов на протяжении многих веков. Но нам нет нужды входить здесь в теоретические тонкости. На ос­нове опыта каждый знает, что Ахиллес догонит черепаху. Посмотрим, как выражается этот факт механики, исходя  из понятия скорости.
Если расстояние между точками А и В равно а, то при дви­жении со скоростью ѵ это расстояние будет пройдено за а\\ѵ сек.
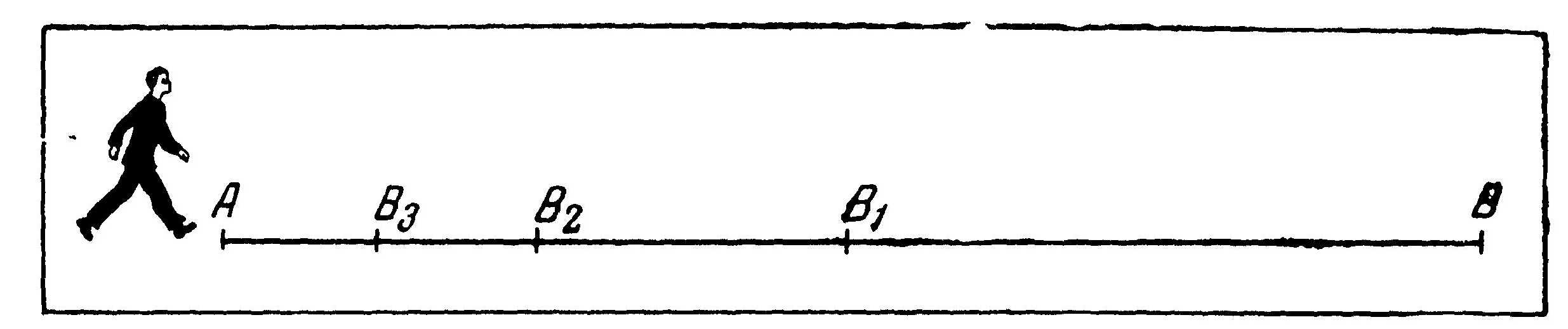
Рассмотрим подробней проблему о дихотомии. Если бы мы достигли точки В1 (см. рис. 7), то осталось бы пройти еще путь длиной а/2 (половину всего пути). При движении со скоростью ѵ это расстояние будет пройдено за
t1 = a/2v сек.
Для прохождения отрезка В2В1 необходимо время
t2 = a/4v сек;
чтобы пройти отрезок B3B2 нужно, чтобы
t3 = a/8v сек;
и т. д. до бесконечности.

Апории Зенона были предметом размышления мате­матиков и философов на протяжении многих веков. Но нам нет нужды входить здесь в теоретические тонкости. На ос­нове опыта каждый знает, что Ахиллес догонит черепаху. Посмотрим, как выражается этот факт механики, исходя  из понятия скорости.
Если расстояние между точками А и В равно а, то при дви­жении со скоростью ѵ это расстояние будет пройдено за а\\ѵ сек.
Рассмотрим подробней проблему о дихотомии. Если бы мы достигли точки В1 (см. рис. 7), то осталось бы пройти еще путь длиной а/2 (половину всего пути). При движении со скоростью ѵ это расстояние будет пройдено за
t1 = a/2v сек.
Для прохождения отрезка В2В1 необходимо время
t2 = a/4v сек;
чтобы пройти отрезок B3B2 нужно, чтобы
t3 = a/8v сек;
и т. д. до бесконечности.
Сложив все эти промежутки, получим время, затраченное на то, чтобы пройти путь АВ,

Сумма в скобках есть бесконечная геометрическая прогрессия со знаменателем 1/2. Как известно, сумма такой прогрессии равна двум. Следовательно, из предыдущего равенства получим, что
t=a/ѵ
Аналогично решается проблема Ахиллеса и черепахи. Если скорость Ахиллеса V, а скорость черепахи — v и если черепаха начинает ползти, находясь впереди Ахиллеса на расстоянии s, то через
 

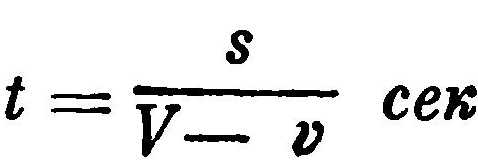
Ахиллес догонит черепаху.
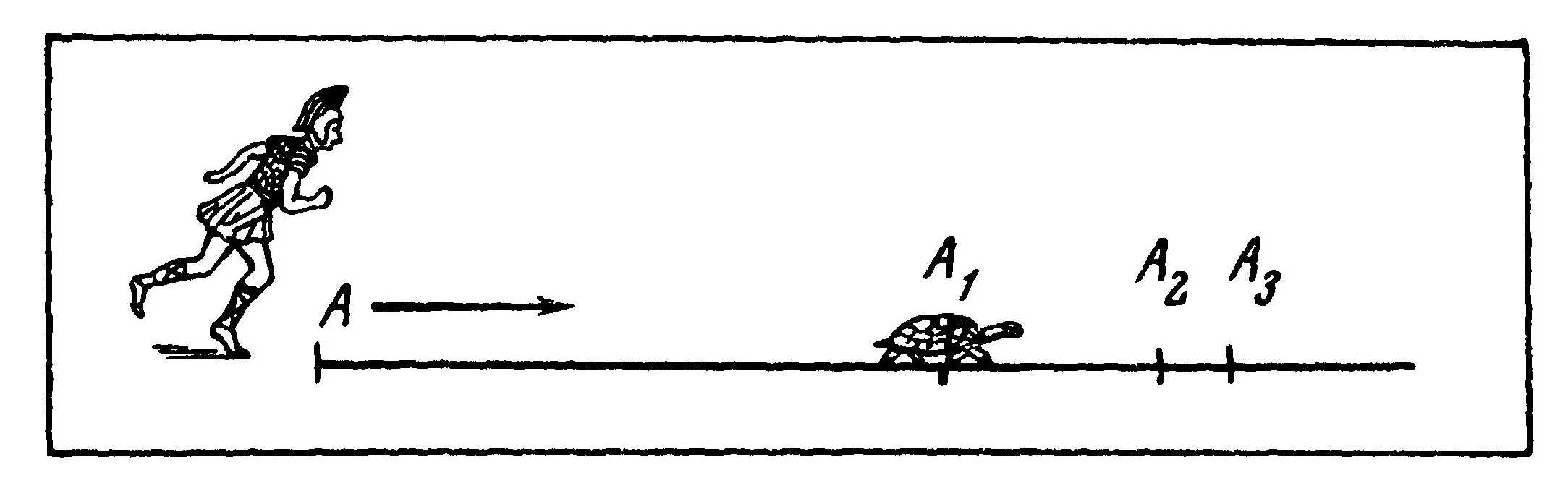
Действительно, Ахиллес добежит из точки А в точку А1 (см.  рис. 8) за
t1=s/V сек
За это время черепаха переползет в точку А2, преодолев расстояние

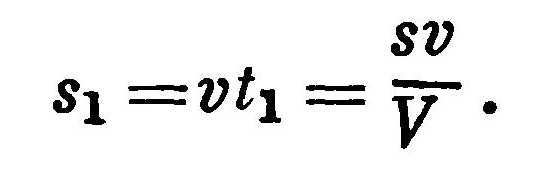
Время, необходимое Ахиллесу, чтобы прибежать из A1 в А2 будет

За это время черепаха проползет расстояние s2 от точки А2 до
точки A3

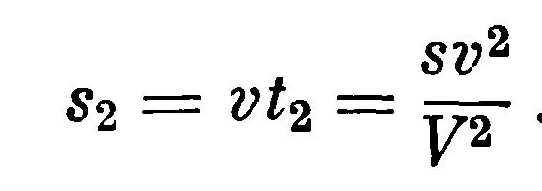
Ахиллес пробежит этот отрезок пути за время

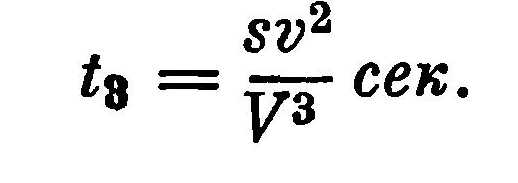
Так можно рассуждать и дальше. Время, которое затратит Ахил­лес, чтобы догнать черепаху, будет равно сумме бесконечного множества промежутков времени t1, t2, t3….

В скобках имеем бесконечную геометрическую прогрессию со зна­менателем v/Ѵ. Используя формулу для суммы этой прогрессии, получим
 

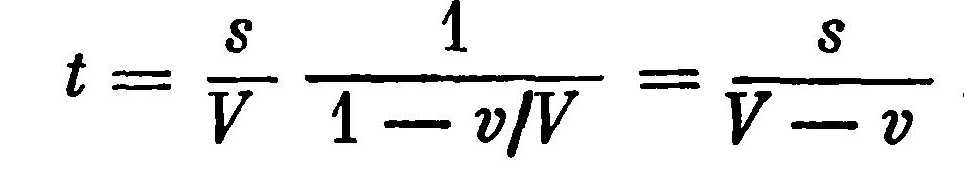
Апорию об Ахиллесе и черепахе приводит на страницах романа «Война и мир» Лев Толстой. Он пишет: «Для человеческого ума непонятна абсолютная непрерывность движения. Человеку становятся понятны законы какого бы то ни было движения только тогда, когда он рассматри­вает произвольно взятые единицы этого движения. Но вме­сте с тем из этого-то произвольного деления непрерывного движения на прерывные единицы проистекает большая часть человеческих заблуждений.
Известен так называемый софизм древних, состоящий в том, что Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идет в десять раз скорее черепахи… Задача эта представлялась древним не­разрешимою. Бессмысленность решения (что Ахиллес ни­когда не догонит черепаху) вытекала из того только, что произвольно были допущены прерывные единицы движе­ния, тогда как движение и Ахиллеса и черепахи соверша­лось непрерывно».
Говоря о математическом решении вопроса об Ахиллесе и черепахе, Толстой пишет дальше:
«Новая отрасль математики, достигнув искусства об­ращаться с бесконечно-малыми величинами, … дает теперь  ответы и на более сложные вопросы, казавшиеся неразре­шимыми. Эта новая, неизвестная древним, отрасль мате­матики… тем самым исправляет ту неизбежную ошибку,  которую ум человеческий не может не делать, рассматри­вая вместо непрерывного движения отдельные единицы движения».
В апории о стреле Зенон допускает ту же самую ошиб­ку, что и в двух первых: он оставляет без внимания свой­ство непрерывности движения. Движение стрелы нельзя рассматривать как сумму состояния покоя: движение более общее явление, чем покой, поэтому его невозможно объяснить только состояниями покоя.
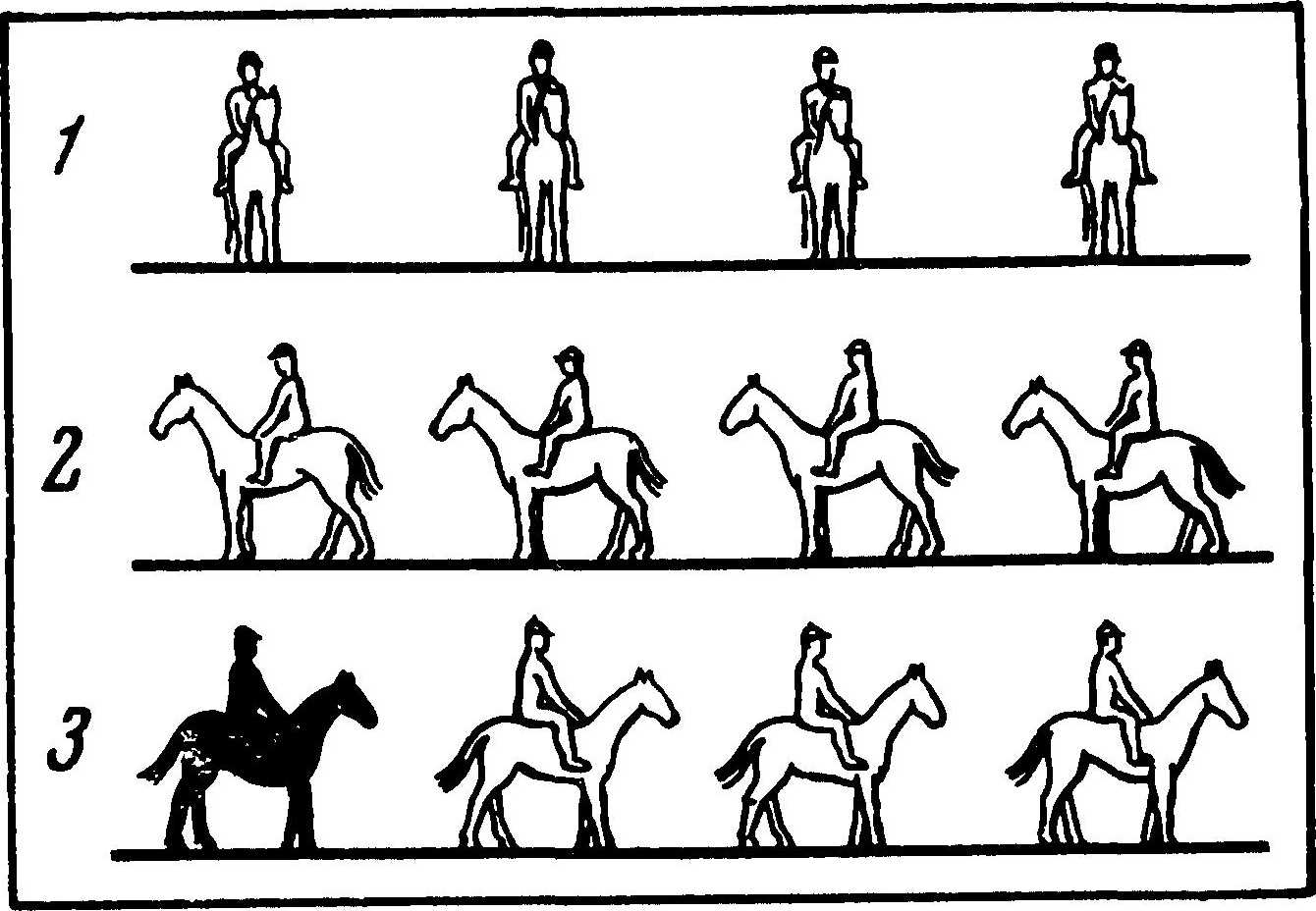
Особенно интересна для нас четвертая апория. Про­тиворечие, к которому пришел здесь Зенон, обусловлено непониманием относительности движения. Эту апорию разрешить несложно.
Пусть второй ряд всадников движется относительно  первого со скоростью ѵ налево, третий ряд — относитель­но первого с такой же скоростью направо. Тогда скорость последнего всадника третьего ряда будет ѵ относительно первого ряда и 2ѵ — относительно второго ряда. Если всадник проскакал t сек, то относительно первого ряда он сдвинулся на vt м, относительно второго — на 2vt м. Здесь мы имеем пример описания движения в различных системах отсчета: в одном случае телом отсчета будет пер­вый ряд всадников, в другом случае — второй. Описание  движения в различных системах отсчета, естественно, дает разные результаты; никаких противоречий этот факт в
себе не содержит.