Классическая механика считала относительной (т. е. зависящей от выбора системы отсчета) скорость. Специальная теория относительности добавила сюда еще промежуток времени и расстояние в пространстве. Вследствие этого ряд понятий, которые мы привыкли считать абсолютными, при ближайшем рассмотрении оказывается относительным. Это относится, в частности, к форме тела. Проиллюстрируем сказанное некоторыми примерами.
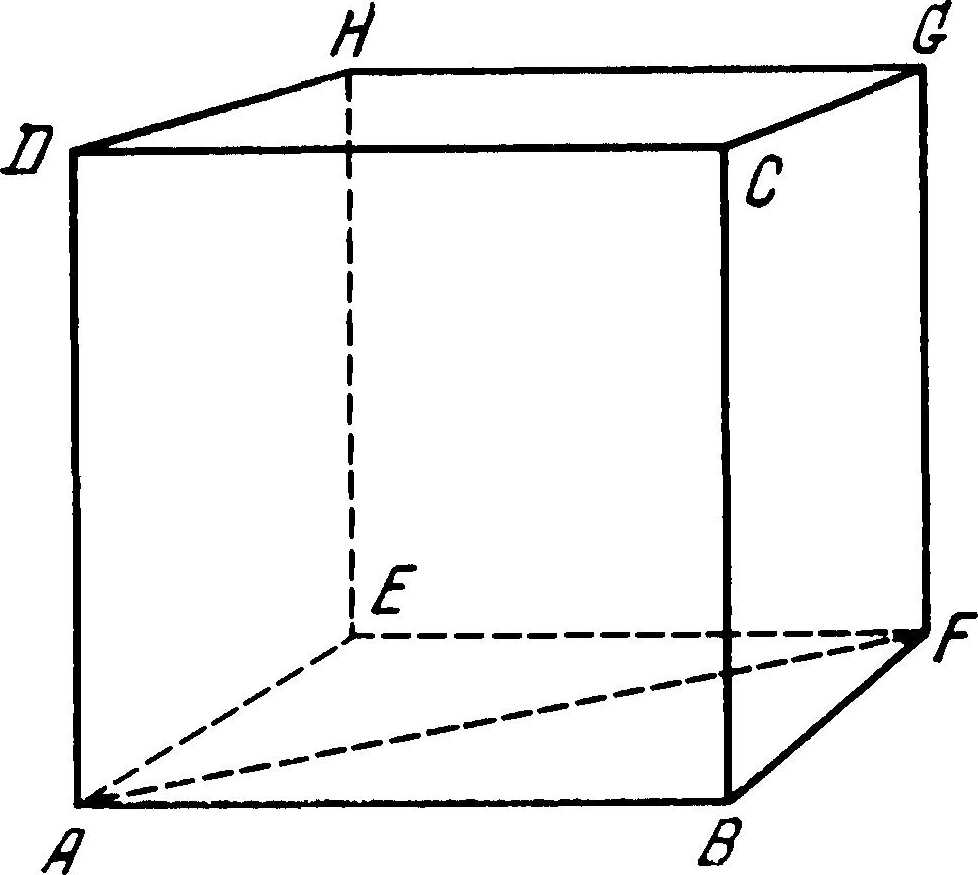
Рис. 34. Куб
Изготовим куб, длина ребра которого равна 1 м, и поставим его на землю (рис 34). Предположим, что над кубом в направлении ребра АВ с большой скоростью проносится самолет. Если летчик измерит размеры куба, то он обнаружит, что ребра куба АВ, EF, DC и HG короче остальных восьми. Таким образом, по мнению летчика, на земле будет стоять не куб, а прямоугольный параллелепипед. Тело, которое в инерциальной системе Земли представляет собой куб, в системе самолета будет прямоугольным параллелепипедом, причем размеры последнего будут зависеть от скорости самолета относительно Земли.
Классическая механика считала относительной (т. е. зависящей от выбора системы отсчета) скорость. Специальная теория относительности добавила сюда еще промежуток времени и расстояние в пространстве. Вследствие этого ряд понятий, которые мы привыкли считать абсолютными, при ближайшем рассмотрении оказывается относительным. Это относится, в частности, к форме тела. Проиллюстрируем сказанное некоторыми примерами.

Рис. 34. Куб
Изготовим куб, длина ребра которого равна 1 м, и поставим его на землю (рис 34). Предположим, что над кубом в направлении ребра АВ с большой скоростью проносится самолет. Если летчик измерит размеры куба, то он обнаружит, что ребра куба АВ, EF, DC и HG короче остальных восьми. Таким образом, по мнению летчика, на земле будет стоять не куб, а прямоугольный параллелепипед. Тело, которое в инерциальной системе Земли представляет собой куб, в системе самолета будет прямоугольным параллелепипедом, причем размеры последнего будут зависеть от скорости самолета относительно Земли.
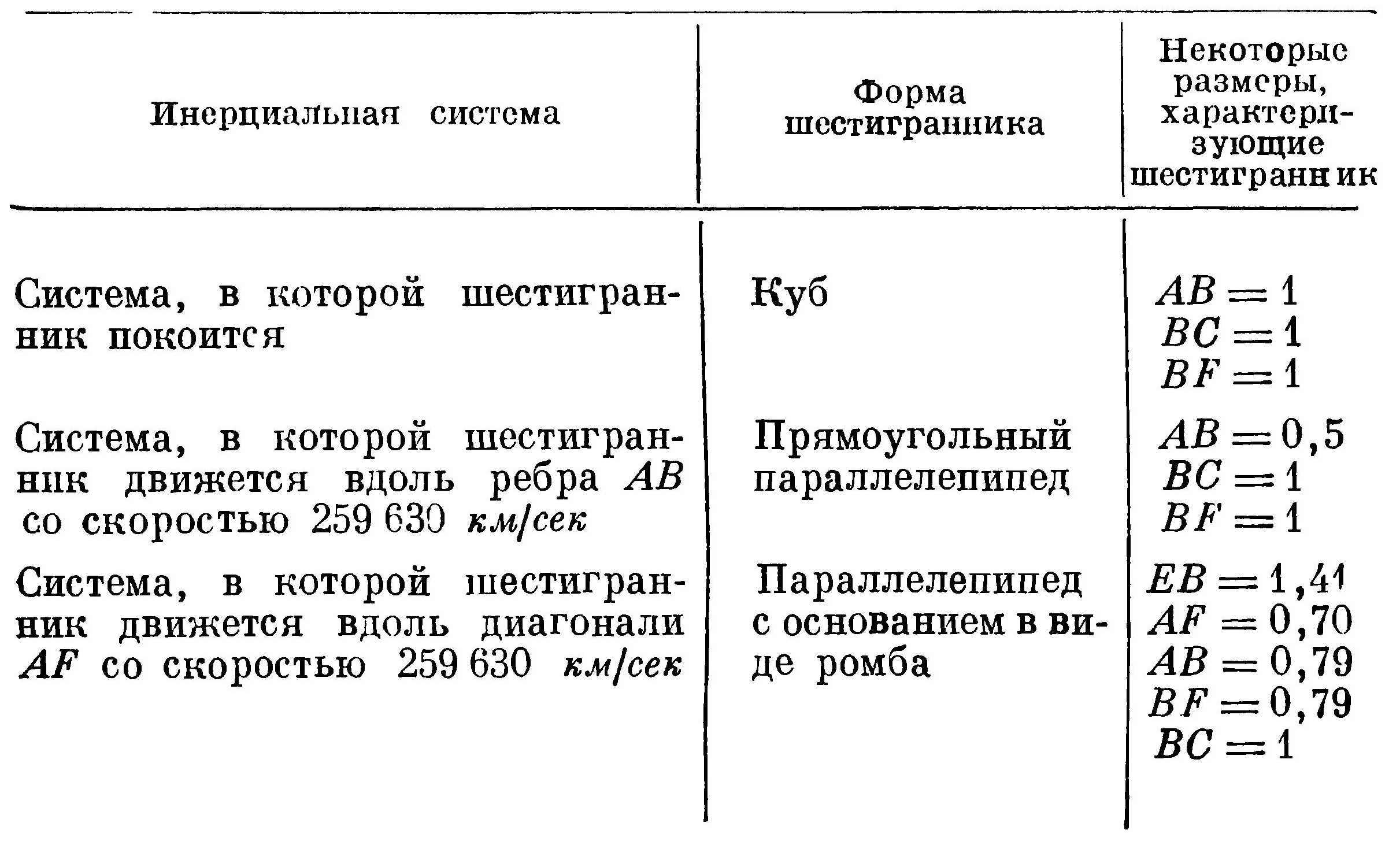
Увидеть вместо куба прямоугольный параллелепипед не единственная возможность. Для летчика, пролетающего над кубом в направлении, отличном от направления АВ, расположенный на земле куб может по форме отличаться и от прямоугольного параллелепипеда. Таким образом, форма шестигранника (который по отношению к Земле является кубом) зависит от инерциальной системы, в которой мы его описываем. Несколько примеров того, как форма шестигранника зависит от инерциальной системы, приведены в табл. 5.
Увидеть вместо куба прямоугольный параллелепипед не единственная возможность. Для летчика, пролетающего над кубом в направлении, отличном от направления АВ, расположенный на земле куб может по форме отличаться и от прямоугольного параллелепипеда. Таким образом, форма шестигранника (который по отношению к Земле является кубом) зависит от инерциальной системы, в которой мы его описываем. Несколько примеров того, как форма шестигранника зависит от инерциальной системы, приведены в табл. 5.
Таблица 5
Размеры шестигранника е различных инерциальных системах
Сказанное выше имеет место не только для шестигранника, но и для тела любой формы. Форма тела всегда зависит от направления и скорости движения. Например, в одной инерциальной системе тело может иметь форму шара, в другой же — форму эллипсоида; в одной системе тело может быть цилиндром вращения, в другой — эллиптическим цилиндром. Форма тела относительна. Только число граней не относительно. Шестигранник всегда останется шестигранником, в какой бы инерциальной системе мы его ни рассматривали.
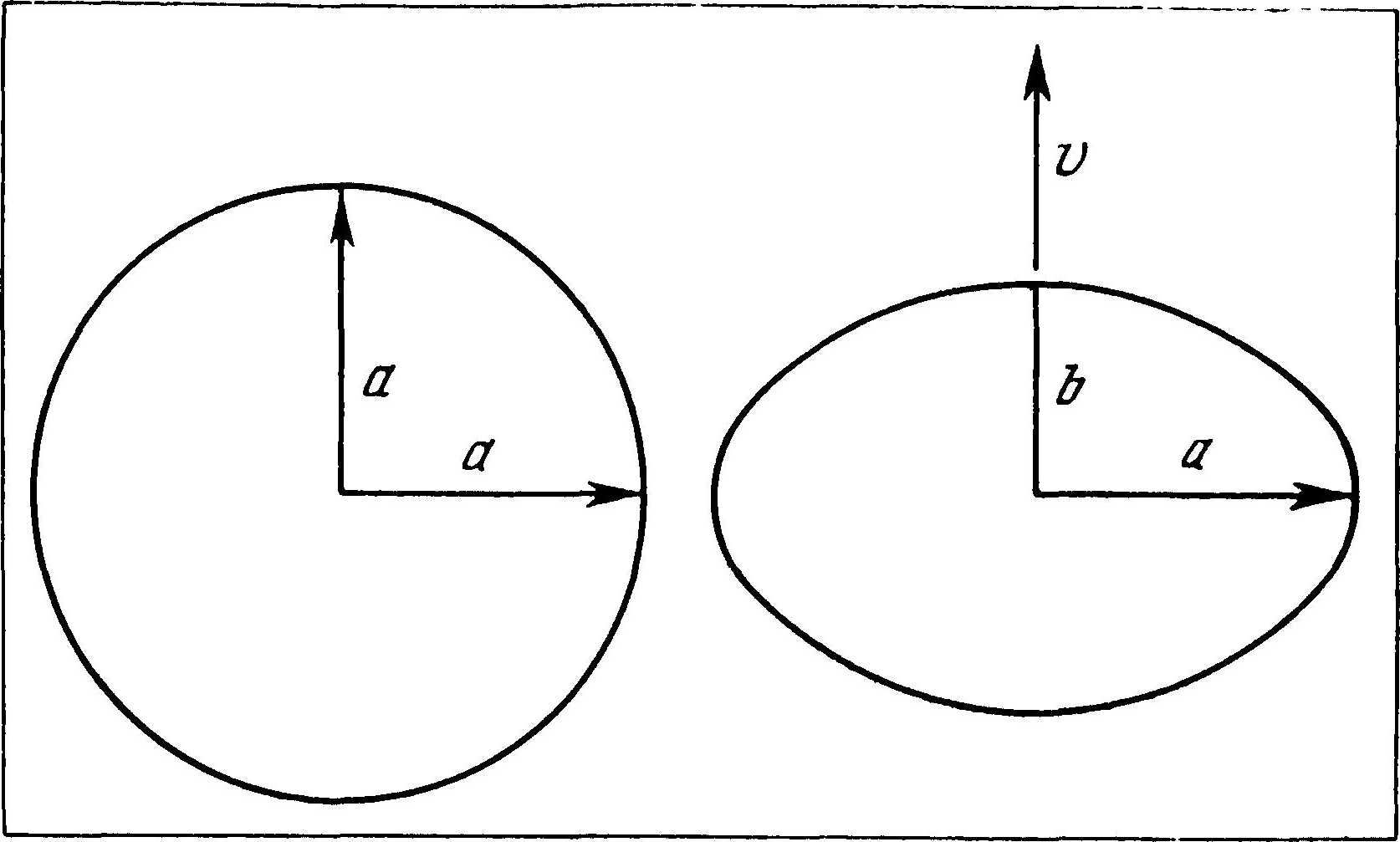
Рис. 35. Если неподвижная фигура является окружностью, то движущаяся будет эллипсом.