Не ведет ли такое следствие теории относительности к противоречиям?
Чтобы ответить на этот вопрос, рассмотрим следующий пример.
Пусть на аэродроме стоят два одинаковых самолета. Предположим далее, что один из них поднимается в воздух, делает крут над городом и с громадной скоростью проносится над самолетом, оставшимся на аэродроме. Наблюдатель, оставшийся на Земле, сравнив размеры летящего самолета с размерами самолета на аэродроме, обнаружит, что пролетевший над аэродромом самолет оказывается короче. Пусть в это же самое время размеры самолетов сравнивает также летчик в воздухе. С его точки зрения его самолет покоится, а аэродром с оставшимся на нем самолетом мчится ему навстречу. Согласно наблюдениям летчика, самолет на земле оказывается короче самолета в воздухе. Заключения наблюдателя на земле и летчика только кажутся противоречивыми. В этом кажущемся противоречии отражается закон природы: длина тела — понятие относительное. Нельзя говорить о длине тела, не указав, в какой системе отсчета эта длина измерена. Чем быстрее движется тело относительно инерциальной системы, тем короче оно в этой системе. Тело длиннее всего в той системе отсчета, где его скорость равна нулю (напомним, что речь идет все время о размерах тела в направлении движения.).
Чтобы ответить на этот вопрос, рассмотрим следующий пример.
Пусть на аэродроме стоят два одинаковых самолета. Предположим далее, что один из них поднимается в воздух, делает крут над городом и с громадной скоростью проносится над самолетом, оставшимся на аэродроме. Наблюдатель, оставшийся на Земле, сравнив размеры летящего самолета с размерами самолета на аэродроме, обнаружит, что пролетевший над аэродромом самолет оказывается короче. Пусть в это же самое время размеры самолетов сравнивает также летчик в воздухе. С его точки зрения его самолет покоится, а аэродром с оставшимся на нем самолетом мчится ему навстречу. Согласно наблюдениям летчика, самолет на земле оказывается короче самолета в воздухе. Заключения наблюдателя на земле и летчика только кажутся противоречивыми. В этом кажущемся противоречии отражается закон природы: длина тела — понятие относительное. Нельзя говорить о длине тела, не указав, в какой системе отсчета эта длина измерена. Чем быстрее движется тело относительно инерциальной системы, тем короче оно в этой системе. Тело длиннее всего в той системе отсчета, где его скорость равна нулю (напомним, что речь идет все время о размерах тела в направлении движения.).
Чем больше скорость тела, тем короче оно по сравнению с другим точно таким же, но покоящимся телом. Не ведет ли такое следствие теории относительности к противоречиям?
Чтобы ответить на этот вопрос, рассмотрим следующий пример.
Пусть на аэродроме стоят два одинаковых самолета. Предположим далее, что один из них поднимается в воздух, делает крут над городом и с громадной скоростью проносится над самолетом, оставшимся на аэродроме. Наблюдатель, оставшийся на Земле, сравнив размеры летящего самолета с размерами самолета на аэродроме, обнаружит, что пролетевший над аэродромом самолет оказывается короче. Пусть в это же самое время размеры самолетов сравнивает также летчик в воздухе. С его точки зрения его самолет покоится, а аэродром с оставшимся на нем самолетом мчится ему навстречу. Согласно наблюдениям летчика, самолет на земле оказывается короче самолета в воздухе. Заключения наблюдателя на земле и летчика только кажутся противоречивыми. В этом кажущемся противоречии отражается закон природы: длина тела — понятие относительное. Нельзя говорить о длине тела, не указав, в какой системе отсчета эта длина измерена. Чем быстрее движется тело относительно инерциальной системы, тем короче оно в этой системе. Тело длиннее всего в той системе отсчета, где его скорость равна нулю (напомним, что речь идет все время о размерах тела в направлении движения.).
Как и все явления, предсказанные теорией относительности, сокращение тел в направлении движения незаметно при малых скоростях. Для велосипедиста, развивающего, например, скорость 18 км/час относительно шоссе, все земные предметы будут сокращаться в направлении его движения только на 0,000 000 000 000 01 %. Если смотреть с самолета, летящего со скоростью 500 км/час, предметы на поверхности земли окажутся укороченными на 0,000 000 000 01%. Это значит, что, например, расстояние между Таллином и Тарту пассажиру этого самолета будет казаться всего лишь на 1,5 стотысячных миллиметра короче, чем показывают наземные измерения. Даже скорости небесных тел слишком малы для того, чтобы можно было обнаружить сокращения, вызванные этими движениями. Солнце, например, движется относительно Земли со скоростью 30 км/сек. Обусловленное этим движением процентное сокращение диаметра Солнца в направлении движения составит 0,000000 5%, т. е. всего-навсего 7 м. При измерении расстояния в 150 млн. км, отделяющего нас от Солнца, такая малая величина вообще несущественна.
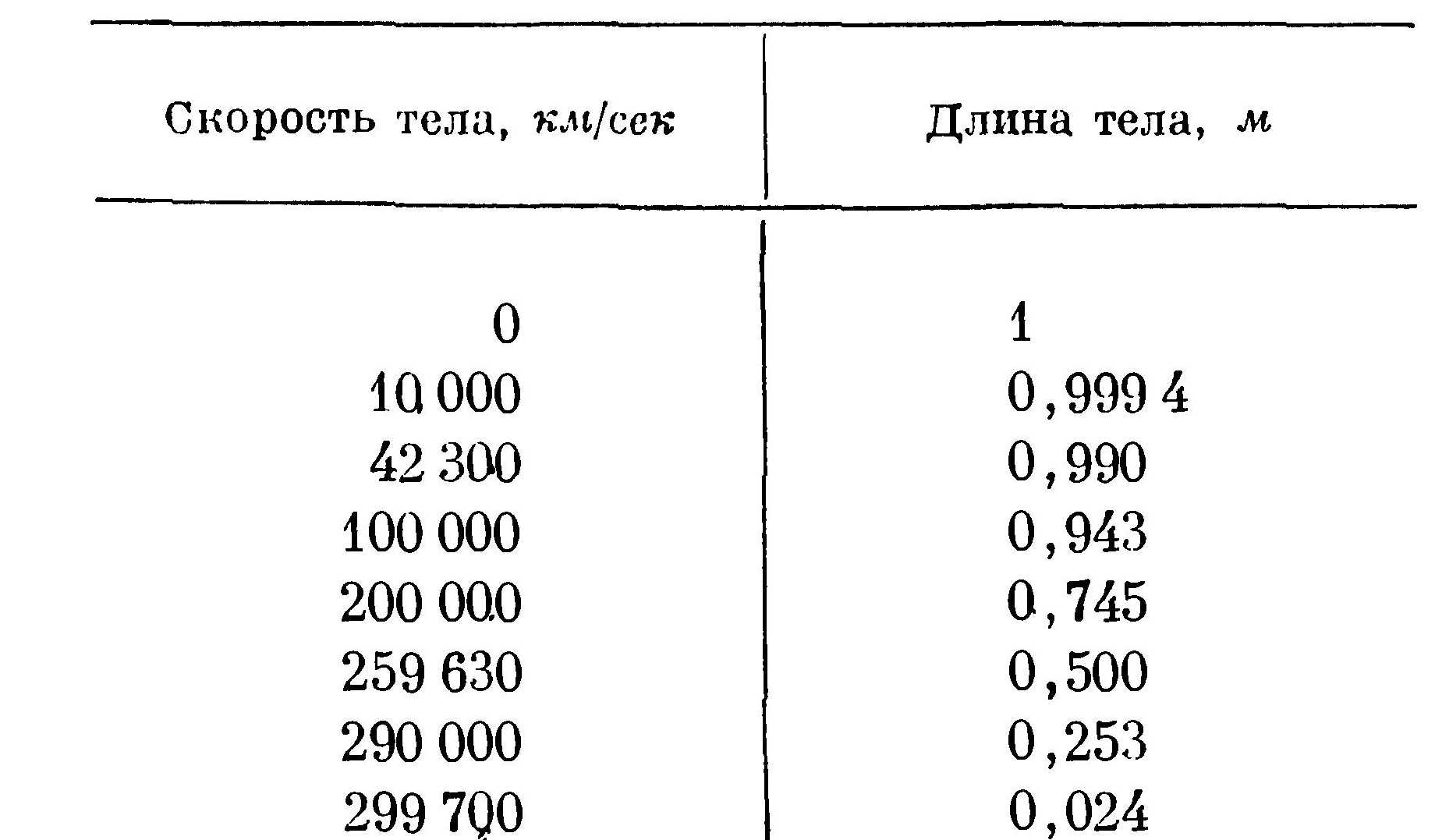
Для скоростей, сравнимых со скоростью света, сокращение тел в направлении движения должно быть заметным. В табл. 4 представлена зависимость длины от скорости для случая, когда длина неподвижного тела равна одному метру.
Чтобы ответить на этот вопрос, рассмотрим следующий пример.
Пусть на аэродроме стоят два одинаковых самолета. Предположим далее, что один из них поднимается в воздух, делает крут над городом и с громадной скоростью проносится над самолетом, оставшимся на аэродроме. Наблюдатель, оставшийся на Земле, сравнив размеры летящего самолета с размерами самолета на аэродроме, обнаружит, что пролетевший над аэродромом самолет оказывается короче. Пусть в это же самое время размеры самолетов сравнивает также летчик в воздухе. С его точки зрения его самолет покоится, а аэродром с оставшимся на нем самолетом мчится ему навстречу. Согласно наблюдениям летчика, самолет на земле оказывается короче самолета в воздухе. Заключения наблюдателя на земле и летчика только кажутся противоречивыми. В этом кажущемся противоречии отражается закон природы: длина тела — понятие относительное. Нельзя говорить о длине тела, не указав, в какой системе отсчета эта длина измерена. Чем быстрее движется тело относительно инерциальной системы, тем короче оно в этой системе. Тело длиннее всего в той системе отсчета, где его скорость равна нулю (напомним, что речь идет все время о размерах тела в направлении движения.).
Как и все явления, предсказанные теорией относительности, сокращение тел в направлении движения незаметно при малых скоростях. Для велосипедиста, развивающего, например, скорость 18 км/час относительно шоссе, все земные предметы будут сокращаться в направлении его движения только на 0,000 000 000 000 01 %. Если смотреть с самолета, летящего со скоростью 500 км/час, предметы на поверхности земли окажутся укороченными на 0,000 000 000 01%. Это значит, что, например, расстояние между Таллином и Тарту пассажиру этого самолета будет казаться всего лишь на 1,5 стотысячных миллиметра короче, чем показывают наземные измерения. Даже скорости небесных тел слишком малы для того, чтобы можно было обнаружить сокращения, вызванные этими движениями. Солнце, например, движется относительно Земли со скоростью 30 км/сек. Обусловленное этим движением процентное сокращение диаметра Солнца в направлении движения составит 0,000000 5%, т. е. всего-навсего 7 м. При измерении расстояния в 150 млн. км, отделяющего нас от Солнца, такая малая величина вообще несущественна.
Для скоростей, сравнимых со скоростью света, сокращение тел в направлении движения должно быть заметным. В табл. 4 представлена зависимость длины от скорости для случая, когда длина неподвижного тела равна одному метру.
Таблица 4
Зависимость длины тела от скорости в направлении движения
Наглядно зависимость сокращения тела в направлении движения изображена на рис 33. На левом краю рисунка изображен стержень такой длины, которую он имеет, будучи неподвижным. Если мы хотим определить длину этого стержня, когда он движется (концом вперед) со скоростью, скажем, 100 000 км/сек, то достаточно измерить расстояние от кривой до точки на горизонтальной оси, где указано число 100 000. Это и будет соответствовать длине стержня, движущегося со скоростью 100 000 км/сек.
На рисунке видно, что, когда скорость тела приближается к скорости света, длина стержня стремится к нулю.
На рисунке видно, что, когда скорость тела приближается к скорости света, длина стержня стремится к нулю.
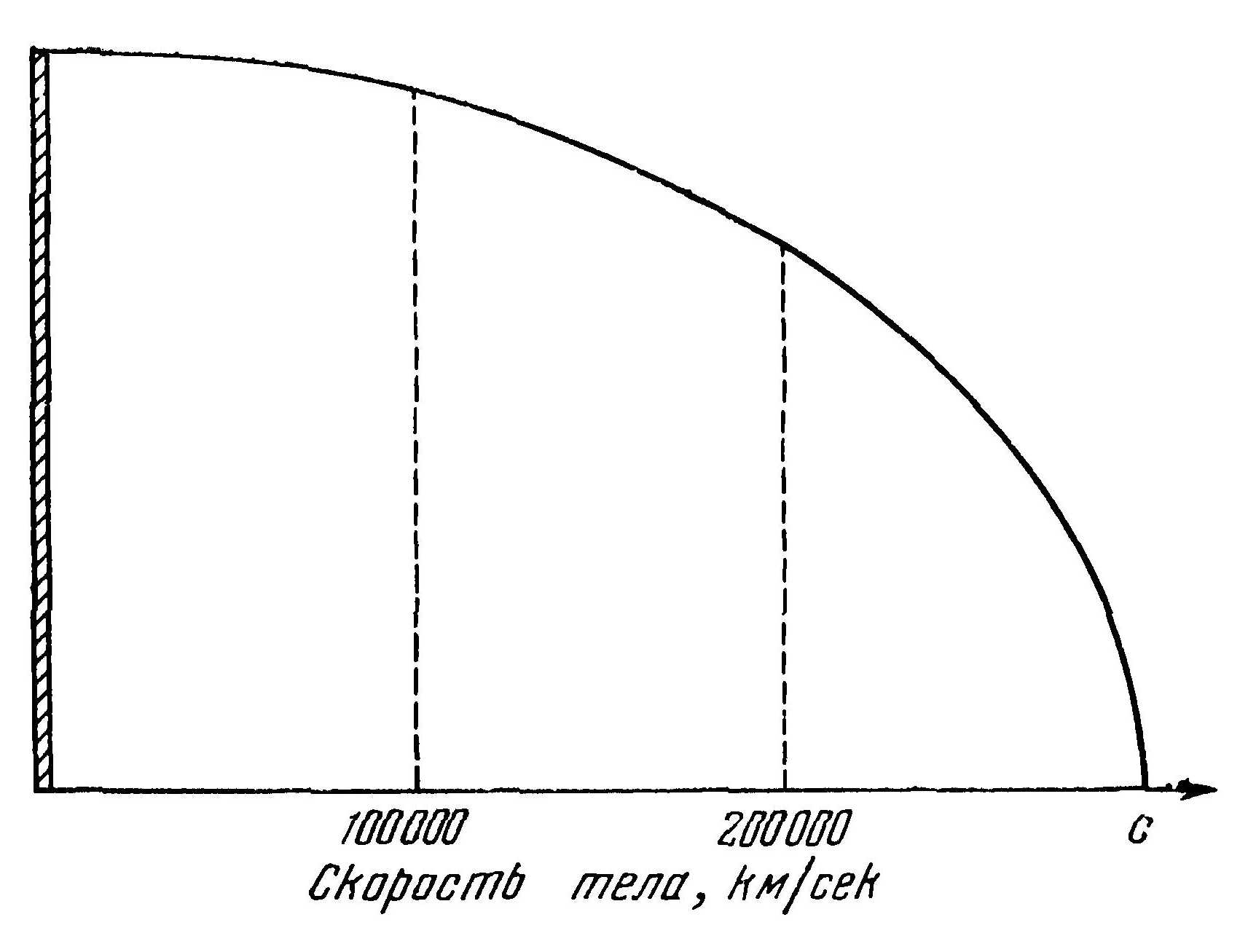
Рис. 33. Зависимость длины тела от скорости
Если бы стержень двигался точно со скоростью света, то его длина была бы равна нулю, т. е. стержень перестал бы существовать. Отсюда видно, что скорость любого тела всегда должна быть меньше скорости света. Со скоростью света могут двигаться только такие объекты, которые не имеют геометрической формы.
Таковы, например, «частицы» света — фотоны, о которых будет идти речь ниже.